Prostokątny trapez: wszystkie formuły i przykłady zadań
Zadania z trapezem nie wydają się trudne w wielu liczbach, które badano wcześniej. W szczególnym przypadku rozważa się prostokątny trapez. Szukając tego obszaru, czasami wygodniej jest podzielić go na dwie już znane: prostokąta i trójkąta. Trzeba tylko trochę pomyśleć i istnieje rozwiązanie.
Definicja prostokątnego trapezu i jego właściwości
Na dowolnym trapezie, podstawy są równoległe, a boki mogą mieć dowolną wartość kątów do nich. Jeżeli rozważany jest prostokątny trapez, wówczas jedna z jego stron jest zawsze prostopadła do podstawy. Oznacza to, że dwa rogi w nim będą równe 90 stopni. Co więcej, zawsze należą one do sąsiednich wierzchołków lub, innymi słowy, na jedną stronę.
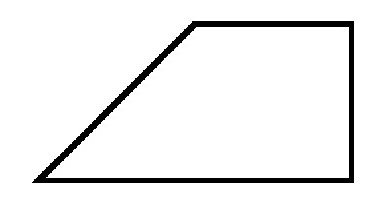
Inne kąty w prostokątnym trapezie są zawsze ostre i tępe. Ich suma będzie zawsze równa 180 stopni.
Każda przekątna tworzy mniejszą stronę trójkąt prostokątny. A wysokość, która jest pobierana od góry z kątem rozwartym, dzieli figurę na dwie. Jeden to prostokąt, a drugi to trójkąt prostokątny. Nawiasem mówiąc, ta strona jest zawsze równa wysokości trapezu.
Jakie oznaczenia są akceptowane w przedstawionych formułach?
Wszystkie wartości używane w różnych wyrażeniach opisujących trapez są dogodnie określone natychmiast i przedstawione w tabeli:
| Wielkość | Jego oznaczenie |
| a | większa podstawa |
| b | mniejsza podstawa prostokątnego trapezu |
| c, h | prostopadle do podstawy, wysokość |
| d | pochyła strona |
| α | kąt ostry |
| β | kąt rozwarty |
| m | środkowa linia trapezu |
| d 1 | mniejsza przekątna |
| d 2 | duża przekątna |
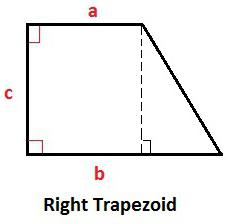
Formuły opisujące elementy prostokątnego trapezu
Najprostszy z nich dotyczy wysokości i mniejszego boku:
c = h.
Jeszcze kilka formuł po tej stronie prostokątnego trapezu:
c = d * sinα;
c = (a - b) * tg α;
c = √ (d 2 - (a - b) 2 ).
Pierwszy wynika z trójkąta prostokątnego. I mówi, że noga do przeciwprostokątnej daje sinus o przeciwnym kącie.
W tym samym trójkącie druga noga jest równa różnicy dwóch zasad. W związku z tym twierdzenie, że równa się styczną kąta do stosunku nóg jest prawdziwe.
Z tego samego trójkąta można wyprowadzić formułę opartą na znajomości twierdzenia Pitagorasa. To jest trzecie zarejestrowane wyrażenie.
Formuły dla drugiej strony można zapisać. Są także trzy:
d = (a - b) / cosα;
d = c / sin α;
d = √ (c 2 + (a - b) 2 ).
Pierwsze dwa są ponownie otrzymywane ze współczynnika kształtu w tym samym trójkącie prostokątnym, a drugie pochodzi z twierdzenia Pitagorasa.
Jakiej formuły można użyć do obliczenia powierzchni?
To, co jest podane dla arbitralnego trapezu. Trzeba tylko wziąć pod uwagę, że wysokość jest bokiem prostopadłym do podstawy.
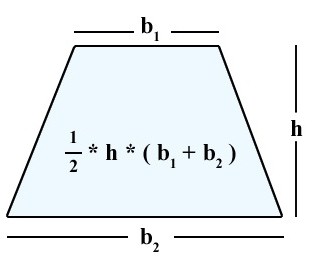
S = (a + b) * h / 2.
Wartości te nie zawsze są podane wprost. Dlatego, aby obliczyć obszar prostokątnego trapezu, należy wykonać pewne obliczenia matematyczne.
Co zrobić, jeśli musisz obliczyć przekątną?
W tym przypadku musisz zobaczyć, że tworzą one dwa trójkąty prostokątne. Dlatego zawsze możesz użyć twierdzenia Pitagorasa. Następnie pierwsza przekątna zostanie wyrażona jako:
d1 = √ (c 2 + b 2 )
lub w inny sposób, zastępując "od" przez "h":
d1 = √ (h 2 + b 2 ).
Podobnie otrzymuje się wzory dla drugiej przekątnej:
d2 = √ (c 2 + b 2 ) lub d 2 = √ (h 2 + a 2 ).
Numer problemu 1
Stan Obszar prostokątnego trapezu jest znany i wynosi 120 dm 2 . Jego wysokość wynosi 8 dm. Konieczne jest obliczenie wszystkich boków trapezu. Dodatkowym warunkiem jest to, że jedna podstawa jest mniejsza od drugiej o 6 dm.
Decyzja. Ponieważ podano prostokątny trapez, w którym wysokość jest znana, możemy od razu powiedzieć, że jedna strona jest równa 8 dm, czyli mniejsza strona.
Teraz możesz policzyć drugą: d = √ (z 2 + (a - b) 2 ). I tu zarówno strona, jak i różnica zasad są natychmiast podawane. Ta ostatnia wynosi 6 dm, jest to znane z tego warunku. Wtedy d będzie równy pierwiastek kwadratowy od (64 + 36), czyli od 100. Więc znalazłem inną stronę, równą 10 dm.
Suma podstaw można znaleźć na podstawie wzoru dla obszaru. Będzie równa dwukrotności wartości obszaru podzielonej przez wysokość. Jeśli się policzysz, okazuje się, że 240/8, dlatego suma podstaw wynosi 30 dm. Z drugiej strony różnica ich wynosi 6 dm. Łącząc te równania, możemy liczyć obie podstawy:
a + b = 30 i a - b = 6.
Możesz wyrazić jako (b + 6), zastąpić go w pierwszej równości. Wtedy okazuje się, że 2b będzie równe 24. Dlatego właśnie b będzie 12 dm.
Następnie ostatnia strona a jest równa 18 dm.
Odpowiedź jest. Boki prostokątnego trapezu: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.
Numer problemu 2
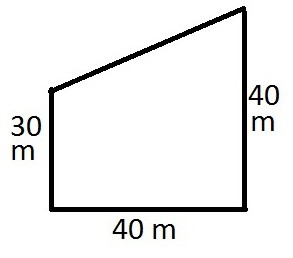
Stan Mając prostokątny trapez. Jego duża strona równa się sumie podstaw. Jego wysokość wynosi 12 cm, zbudowany jest prostokąt, którego boki są równe podstawie trapezu. Konieczne jest obliczenie obszaru tego prostokąta.
Decyzja. Musisz zacząć od pożądanego. Wymagany obszar jest określony jako iloczyn aib. Obie te wielkości nie są znane.
Będzie wymagać użycia dodatkowych równości. Jedna z nich opiera się na stwierdzeniu z warunku: d = a + b. Konieczne jest użycie trzeciej formuły dla tej strony, która jest podana powyżej. Okazuje się, że: d 2 = c 2 + (a - b) 2 lub (a + b) 2 = c 2 + (a - b) 2 .
Konieczne jest dokonanie transformacji, zastępując zamiast jej warunek z warunku - 12. Po otwarciu nawiasów i odlewania takich terminów okazuje się, że 144 = 4 ab.
Na początku decyzji powiedziano, że a * b daje wymagany obszar. Dlatego w ostatnim wyrażeniu można zastąpić ten produkt przez S. Proste obliczenie da wartość obszaru. S = 36 cm 2 .
Odpowiedź jest. Wymagany obszar to 36 cm 2 .
Numer problemu 3
Stan Powierzchnia prostokątnego trapezu 150√3 cm². Ostry kąt wynosi 60 stopni. Kąt między małą podstawą a mniejszą przekątną ma tę samą wartość. Konieczne jest obliczenie mniejszej przekątnej.
Decyzja. Z własności kątów trapezowych okazuje się, że kąt rozwarty wynosi 120 °. Następnie przekątna dzieli go na równe, ponieważ jedna jego część ma już 60 stopni. Następnie kąt między tą przekątną a drugą podstawą wynosi również 60 stopni. Oznacza to, że trójkąt utworzony przez dużą podstawę, pochyłą stronę i mniejszą przekątną jest równoboczny. Tak więc pożądana przekątna będzie równa a, jak również stronie d = a.
Teraz musimy wziąć pod uwagę trójkąt prostokątny. W nim trzeci kąt wynosi 30 stopni. Noga leżąca na niej równa jest połowie przeciwprostokątnej. Oznacza to, że mniejsza podstawa trapezu jest równa połowie pożądanej przekątnej: b = a / 2. Z tego należy znaleźć wysokość równą stronie, prostopadłą do podstaw. Strona z tutaj to noga. Z twierdzenia Pitagorasa:
c = (a / 2) * √3.
Pozostaje tylko zastąpić wszystkie wartości w formule obszaru:
150√3 = (a + a / 2) * (a / 2 * √3) / 2.
Rozwiązanie tego równania daje root z 20
Odpowiedź jest. Mniejsza przekątna ma 20 cm długości.