Równanie regresji Równanie regresji wielokrotnej

Podczas studiów uczniowie często spotykają się z różnymi równaniami. Jeden z nich - równanie regresji - jest rozważany w tym artykule. Ten typ równania jest używany specjalnie do opisania charakterystyki zależności między parametrami matematycznymi. Ten rodzaj równości wykorzystywany jest w statystykach i ekonometrii.

Definicja regresji

W matematyce regresja odnosi się do pewnej wartości opisującej zależność średniej wartości całych danych od wartości innej wartości. Równanie regresji pokazuje średnią wartość innego atrybutu jako funkcji określonego atrybutu. Funkcja regresji ma postać prostego równania y = x, w którym y jest zmienną zależną, a x jest niezależne (współczynnik znaku). W rzeczywistości regresja wyrażana jest jako y = f (x).

Jakie są typy relacji między zmiennymi?

Ogólnie wyróżniają się dwa przeciwne typy wzajemnych połączeń: korelacja i regresja.

Pierwszy charakteryzuje się równością zmiennych warunkowych. W tym przypadku nie jest pewne, która zmienna zależy od innej.

Jeśli nie ma równości między zmiennymi iw warunkach jest powiedziane, która zmienna objaśnia i która jest zależna, wówczas możemy mówić o obecności drugiego typu połączenia. Aby skonstruować równanie regresji liniowej, konieczne będzie ustalenie, jaki typ relacji obserwuje się.

Rodzaje regresji

Do chwili obecnej istnieje 7 różnych typów regresji: hiperboliczny, liniowy, wielokrotny, nieliniowy, pary, odwrotny, logarytmicznie liniowy.

Hiperboliczny, liniowy i logarytmiczny

Równanie liniowe Regresje są używane w statystykach do jasnego objaśnienia parametrów równania. Wygląda na to, że y = c + t * x + e. Równanie hiperboliczne ma postać regularnej hiperboli: y = c + t / x + E. Logarytmicznie liniowe równanie wyraża zależność za pomocą funkcji logarytmicznej: In y = In c + t * In x + In E.

Liczba mnoga i nieliniowa

Dwa bardziej złożone rodzaje regresji są wielokrotne i nieliniowe. Równanie regresji wielokrotnej wyrażone jest przez funkcję y = f (x ₁ , x ₂ ... x _c ) + E. W tej sytuacji y jest zmienną zależną, a x jest zmienną objaśniającą. Zmienna E jest stochastyczna, zawiera wpływ innych czynników w równaniu. Równanie regresji nieliniowej jest nieco sprzeczne. Z jednej strony, biorąc pod uwagę brane pod uwagę wskaźniki, nie jest on liniowy, ale z drugiej strony, w roli wskaźników ewaluacyjnych jest liniowy.

Odwrotne i sparowane typy regresji

Odwrotność jest rodzajem funkcji, którą należy przekształcić w formę liniową. W najbardziej tradycyjnych aplikacjach ma postać funkcji y = 1 / s + t * x + E. Równanie regresji parami demonstruje związek między danymi w funkcji y = f (x) + E. Podobnie jak w innych równaniach, y zależy od x, a E jest parametrem stochastycznym.

Pojęcie korelacji

Jest to wskaźnik, który pokazuje istnienie związku między dwoma zjawiskami lub procesami. Siła związku wyrażona jest jako współczynnik korelacji. Jego wartość zmienia się w przedziale [-1; +1]. Ujemny wskaźnik wskazuje na obecność sprzężenia zwrotnego, a pozytywny wskazuje na bezpośredni. Jeśli współczynnik przyjmuje wartość 0, nie ma związku. Im bliżej wartości 1, tym silniejsze połączenie między parametrami, im bliżej 0, tym słabsze.

Metody

Korelacja metod parametrycznych może ocenić bliskość relacji. Są one stosowane na podstawie oszacowania dystrybucji w celu zbadania parametrów zgodnych z prawem rozkładu normalnego.

Parametry równania regresji liniowej są potrzebne do określenia typu zależności, funkcji równania regresji i oceny wskaźników wybranej formuły wzajemnych zależności. Pole korelacji służy jako metoda identyfikacji komunikacji. Aby to zrobić, wszystkie istniejące dane muszą być wyświetlane graficznie. W prostokątnym, dwuwymiarowym układzie współrzędnych konieczne jest zastosowanie wszystkich znanych danych. Tworzy to pole korelacji. Wartość współczynnika opisującego zaznaczona jest na osi odciętych, a wartości współczynnika zależnego zaznaczone są wzdłuż osi rzędnych. Jeśli istnieje zależność funkcjonalna między parametrami, są one ułożone w postaci linii.

Jeśli współczynnik korelacji takich danych jest mniejszy niż 30%, można mówić o prawie całkowitym braku komunikacji. Jeśli wynosi od 30% do 70%, oznacza to obecność ogniw o średniej szczelności. 100% wskaźnik - dowód komunikacji funkcjonalnej.

Równanie regresji nieliniowej, a także liniowej, należy uzupełnić indeksem korelacji (R).

Korelacja wielokrotnej regresji

Współczynnik determinacji jest wskaźnikiem kwadratu wielokrotnej korelacji. Mówi o bliskości związku prezentowanego zestawu wskaźników z badaną cechą. Potrafi także mówić o naturze wpływu parametrów na wynik. Równanie regresji wielokrotnej szacuje się za pomocą tego wskaźnika.

Aby obliczyć wskaźnik korelacji wielokrotnej, należy obliczyć jego indeks.

Metoda najmniejszych kwadratów

Ta metoda jest metodą szacowania współczynników regresji. Jego istotą jest minimalizacja sumy odchyleń w kwadracie, uzyskanych z powodu zależności czynnika od funkcji.

Równanie regresji liniowej parami można oszacować za pomocą tej metody. Ten typ równań stosuje się w przypadku wykrywania między wskaźnikami liniowej zależności parami.

Parametry równań

Każdy parametr funkcji regresji liniowej ma określone znaczenie. Równanie parowania regresji liniowej zawiera dwa parametry: s oraz m. Parametr t pokazuje średnią zmianę końcowego wskaźnika funkcji y, z zastrzeżeniem zmniejszenia (zwiększenia) zmiennej x przez jedną konwencjonalną jednostkę. Jeśli zmienną x jest zero, funkcja równa się parametrowi c. Jeśli zmienną x nie jest zero, to współczynnik c nie ma sensu ekonomicznego. Jedyny wpływ na funkcję ma znak przed współczynnikiem c. Jeśli istnieje minus, możemy powiedzieć o powolnej zmianie wyniku w stosunku do czynnika. Jeśli występuje plus, oznacza to przyspieszoną zmianę wyniku.

Każdy parametr, który zmienia wartość równania regresji, można wyrazić za pomocą równania. Na przykład współczynnik c ma postać c = y - mx.

Pogrupowane dane

Istnieją takie warunki problemu, w których wszystkie informacje są pogrupowane na podstawie x, ale w tym samym czasie dla określonej grupy wskazane są odpowiednie średnie wartości wskaźnika zależnego. W takim przypadku średnie wartości opisują zmiany indeksu w zależności od x. Zatem pogrupowane informacje pomagają znaleźć równanie regresji. Jest używany jako analiza relacji. Jednak ta metoda ma swoje wady. Niestety, średnie wskaźniki często podlegają zewnętrznym wahaniom. Te oscylacje nie są odzwierciedleniem wzorca relacji, tylko maskują jego "hałas". Średnie pokazują, że wzorce zależności są znacznie gorsze niż równanie regresji liniowej. Można je jednak wykorzystać jako podstawę do znalezienia równania. Mnożąc siłę pojedynczej populacji przez odpowiednią średnią, można uzyskać liczbę y w grupie. Następnie musisz wyrównać wszystkie otrzymane kwoty i znaleźć ostateczny wskaźnik. Nieco trudniej wykonać obliczenia z sumą xy. W takim przypadku, jeśli interwały są małe, można warunkowo przyjąć wskaźnik x dla wszystkich jednostek (w grupie) tak samo. Konieczne jest pomnożenie jej przez sumę y, aby znaleźć sumę iloczynu x przez y. Ponadto wszystkie ilości dodaje się razem i otrzymuje się całkowitą ilość xy.

Wielokrotne równanie regresji parami: oszacowanie znaczenia komunikacji

Jak wcześniej wspomniano, regresja wielokrotna ma funkcję postaci y = f (x ₁ , x ₂ , ..., x _m ) + E. Najczęściej takie równanie służy do rozwiązania problemu podaży i popytu na produkt, dochodu odsetkowego odkupionych akcji, do badania przyczyn i rodzaju funkcji kosztów produkcji. Jest również aktywnie wykorzystywany w wielu różnych badaniach i obliczeniach makroekonomicznych, ale na poziomie mikroekonomicznym takie równanie jest wykorzystywane nieco mniej.

Głównym zadaniem wielokrotnej regresji jest zbudowanie modelu danych zawierającego ogromną ilość informacji w celu dalszego określenia wpływu każdego z czynników osobno iw ich całkowitej całości na modelowany wskaźnik i jego współczynniki. Równanie regresji może przyjmować wiele różnych wartości. Jednocześnie dwa typy funkcji są powszechnie używane do oceny wzajemnego połączenia: liniowego i nieliniowego.

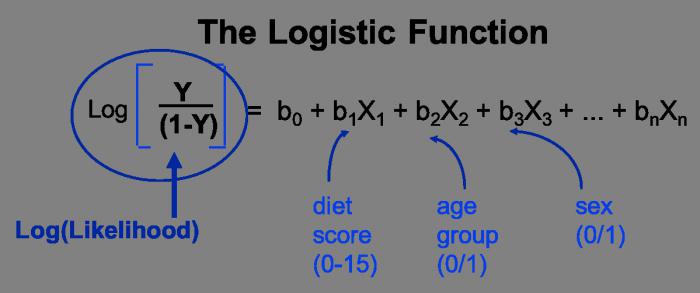
Funkcja liniowa przedstawiona jest w postaci następującej zależności: y = a ₀ + a ₁ x ₁ + a ₂ x ₂ , + ... + a _m x _m . Jednocześnie, _{a2, m} , są uważane za "czyste" współczynniki regresji. Są one niezbędne do scharakteryzowania średniej zmiany parametru y ze zmianą (zmniejszenie lub wzrost) w każdym odpowiednim parametrze x o jedną jednostkę, z warunkiem stabilnej wartości innych wskaźników.

Równania nieliniowe mają na przykład postać funkcji mocy y = oś ₁ ^b1 x ₂ ^b2 ... x _m ^bm . W tym przypadku wywoływane są wskaźniki b ₁ , b ₂ ..... b _m - współczynniki elastyczności pokazują, jak zmienia się wynik (o ile%) wraz ze wzrostem (zmniejszeniem) w odpowiednim wskaźniku x o 1% i ze stabilnym wskaźnikiem pozostałych czynników.

Jakie czynniki należy wziąć pod uwagę przy tworzeniu regresji wielokrotnej

Aby prawidłowo skonstruować regresję wielokrotną, należy dowiedzieć się, na które czynniki należy zwrócić szczególną uwagę.

Konieczne jest zrozumienie natury związku między czynnikami ekonomicznymi a modelem. Czynniki, które należy uwzględnić, muszą spełniać następujące kryteria:

• Powinien podlegać kwantyfikacji. Aby użyć czynnika opisującego jakość obiektu, w każdym przypadku należy podać mu formę ilościową.
• Nie powinno być żadnych wzajemnych korelacji czynników ani relacji funkcjonalnej. Takie działania najczęściej prowadzą do nieodwracalnych konsekwencji - system zwykłych równań staje się bezwarunkowy, a to pociąga za sobą nierzetelność i niejasność szacunków.
• W przypadku istnienia ogromnego wskaźnika korelacji, nie ma możliwości określenia wyizolowanego wpływu czynników na końcowy wynik wskaźnika, dlatego współczynniki stają się niezinterpretowane.

Metody budowy

Istnieje ogromna liczba metod i metod wyjaśniających, jak wybrać czynniki dla równania. Wszystkie te metody są jednak oparte na wyborze współczynników z wykorzystaniem indeksu korelacji. Wśród nich są:

• Metoda eliminacji.
• Metoda włączania.
• Analiza regresji krok po kroku.

Pierwsza metoda polega na wyeliminowaniu wszystkich współczynników z zestawu zbiorczego. Druga metoda polega na wprowadzeniu wielu dodatkowych czynników. Trzeci to eliminacja czynników, które poprzednio były używane do równania. Każda z tych metod ma prawo istnieć. Mają swoje za i przeciw, ale mogą rozwiązać problem eliminowania niepotrzebnych wskaźników na swój własny sposób. Z reguły wyniki uzyskane dla każdej poszczególnej metody są dość bliskie.

Metody analizy wielowymiarowej

Takie metody określania czynników opierają się na uwzględnieniu indywidualnych kombinacji powiązanych ze sobą cech. Obejmują one analizę dyskryminacyjną, rozpoznawanie twarzy, sposób analizy głównych składników i analizę skupień. Ponadto istnieje również analiza czynnikowa jednak pojawił się z powodu rozwoju metody składowej. Wszystkie są używane w pewnych okolicznościach, z zastrzeżeniem pewnych warunków i czynników.