Kilka uwag na temat sposobu rozwiązania problemu nierówności
Jednym z tematów, który wymaga od studentów maksymalnej uwagi i wytrwałości, jest rozwiązanie problemu nierówności. Takie podobne do równań i jednocześnie bardzo różne od nich. Ponieważ ich rozwiązanie wymaga specjalnego podejścia.
Właściwości, które będą wymagane do znalezienia odpowiedzi
Wszystkie z nich są używane do zastąpienia istniejącego rekordu odpowiednikiem. Większość z nich jest podobna do tego, co było w równaniach. Ale są różnice.
- Funkcję zdefiniowaną w LDU lub dowolną liczbę można dodać do obu stron pierwotnej nierówności.
- Podobnie mnożenie jest możliwe, ale tylko przez pozytywną funkcję lub liczbę.
- Jeśli to działanie jest wykonywane z ujemną funkcją lub liczbą, to znak nierówności musi zostać zastąpiony przeciwnym.
- Funkcje, które są nieujemne, mogą zostać podniesione do dodatniej mocy.
Czasom rozwiązaniu nierówności towarzyszą działania, które dają nieistotne odpowiedzi. Należy je wyeliminować, porównując domenę DHS i różnorodne rozwiązania.
Korzystanie z metody odstępów
Jego istotą jest zredukowanie nierówności do równania, w którym po prawej stronie jest zero.
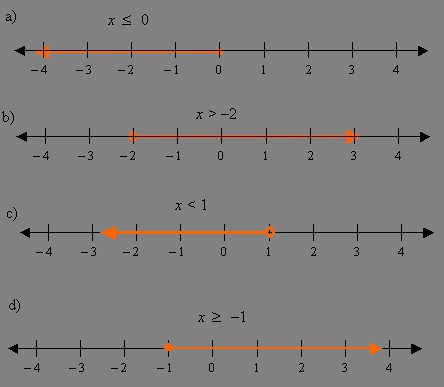
- Określ obszar, w którym znajdują się prawidłowe wartości zmiennych, czyli LDL.
- Przekształć nierówności za pomocą operacji matematycznych, tak aby w jego prawej części było zero.
- Zamień znak nierówności na "=" i rozwiąż odpowiednie równanie.
- Na osi numerycznej zaznacz wszystkie odpowiedzi, które pojawiły się podczas rozwiązania, a także interwały TLD. Przy ścisłej nierówności punktu musisz narysować przebicie. Jeśli istnieje znak równości, to powinny one zamalować.
- Określ znak oryginalnej funkcji na każdym przedziale wynikający z punktów LDD i dzieląc odpowiedzi. Jeśli przy przejściu przez punkt znak funkcji nie ulegnie zmianie, wówczas wchodzi w odpowiedź. W przeciwnym razie - wykluczone.
- Punkty graniczne dla TLD należy dodatkowo sprawdzić, a następnie uwzględnić w odpowiedzi.
- Uzyskana odpowiedź musi być napisana w formie zjednoczonych zbiorów.
Niewiele chodzi o podwójne nierówności
Używają dwóch znaków nierówności w zapisie. Oznacza to, że niektóre funkcje są ograniczone przez warunki natychmiast dwa razy. Takie nierówności są rozwiązywane jako system dwóch, gdy oryginał jest podzielony na części. W metodzie interwałowej wskazane są odpowiedzi z rozwiązania obu równań.
Aby je rozwiązać, dopuszczalne jest stosowanie wyżej wymienionych właściwości. Z ich pomocą wygodnie jest zredukować nierówność do równości zero.

Jaka jest sytuacja z nierównościami, w których istnieje moduł?
W tym przypadku rozwiązanie nierówności wykorzystuje następujące właściwości i są one prawdziwe dla wartości dodatniej "a".
Jeśli "x" przyjmuje wyrażenie algebraiczne, to takie podstawienia są prawdziwe:
- | x | <a do -a <x <a;
- | x | > a na x <-a lub x> a.
Jeśli nierówności nie są ścisłe, wówczas formuły są również prawdziwe, tylko w nich, z wyjątkiem znaku mniej więcej, pojawia się "=".
Jak rozwiązać system nierówności?
Wiedza ta będzie wymagana w przypadkach, w których takie zadanie zostanie podjęte lub odnotowany zostanie podwójny brak równości lub moduł pojawi się w rekordzie. W takiej sytuacji rozwiązaniem byłyby wartości zmiennych, które zaspokajałyby wszystkie nierówności w zapisie. Jeśli nie ma takich liczb, system nie ma rozwiązań.
Plan rozwiązania systemu nierówności:
- rozwiązać każdy z nich osobno;
- narysuj wszystkie interwały na osi numerycznej i określ ich skrzyżowania;
- napisz odpowiedź systemu, która będzie połączeniem tego, co wydarzyło się w drugim akapicie.
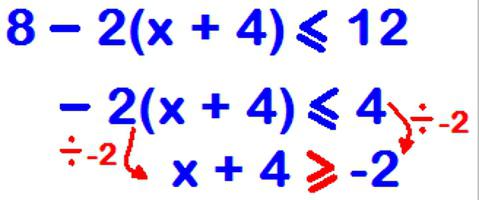
Jak radzić sobie z ułamkowymi nierównościami?
Ponieważ w trakcie ich rozwiązywania może być konieczna zmiana znaku nierówności, konieczne jest bardzo staranne i ostrożne przeprowadzenie wszystkich punktów planu. W przeciwnym razie może to być odpowiedź odwrotna.
Rozwiązanie nierówności ułamkowych również wykorzystuje metodę interwałową. A planem działania będzie:
- Korzystając z opisanych właściwości, należy ułamek taki wyglądać, że tylko zero pozostaje na prawo od znaku.
- Zastąp nierówność "=" i określ punkty, w których funkcja będzie równa zeru.
- Zaznacz je na osi współrzędnych. W takim przypadku liczby wynikające z obliczeń w mianowniku będą zawsze przekłuwane. Wszystkie pozostałe - w oparciu o warunki nierówności.
- Określ przedziały konsystencji.
- W odpowiedzi zapisz związek tych interwałów, których znak odpowiada temu, który był w pierwotnej nierówności.
Sytuacje, w których irracjonalność pojawia się w nierówności
Innymi słowy, w zapisie jest matematyczny pierwiastek. Ponieważ w szkolnym kursie algebry wykonuje się większość zadań pierwiastek kwadratowy to będzie brane pod uwagę.
Rozwiązaniem irracjonalnych nierówności jest uzyskanie systemu dwóch lub trzech, który będzie równoważny z oryginałem.
| Oryginalna nierówność | warunek | równoważny system |
| √ n (x) <m (x) | m (x) jest mniejsze lub równe 0 | brak rozwiązań |
| m (x) większy niż 0 | n (x) jest większe lub równe 0 n (x) <(m (x)) 2 | |
| √ n (x)> m (x) | m (x) jest większe lub równe 0 n (x)> (m (x)) 2 | |
lub n (x) jest większe lub równe 0 m (x) jest mniejsze niż 0 | ||
| √n (x) ≤ m (x) | m (x) jest mniejsze niż 0 | brak rozwiązań |
| m (x) jest większe lub równe 0 | n (x) jest większe lub równe 0 n (x) ≤ (m (x)) 2 | |
| √n (x) ≥ m (x) | m (x) jest większe lub równe 0 n (x) ≥ (m (x)) 2 | |
lub n (x) jest większe lub równe 0 m (x) jest mniejsze niż 0 | ||
| √ n (x) <√ m (x) | n (x) jest większe lub równe 0 n (x) jest mniejsze niż m (x) | |
| √n (x) * m (x) <0 | n (x) jest większe niż 0 m (x) jest mniejsze niż 0 | |
| √n (x) * m (x)> 0 | n (x) jest większe niż 0 m (x) większy niż 0 | |
| √n (x) * m (x) ≤ 0 | n (x) jest większe niż 0 m (x) ≤0 | |
lub n (x) wynosi 0 m (x) - dowolny | ||
| √n (x) * m (x) ≥ 0 | n (x) jest większe niż 0 m (x) ≥0 | |
lub n (x) wynosi 0 m (x) - dowolny |
Przykłady rozwiązywania różnych typów nierówności
Aby dodać jasność do teorii rozwiązania nierówności, poniżej znajdują się przykłady.
Pierwszy przykład. 2x - 4> 1 + x
Rozwiązanie: aby określić TLD, wystarczy przyjrzeć się bliżej nierówności. Jest utworzony z funkcji liniowych, dlatego jest zdefiniowany dla wszystkich wartości zmiennej.
Teraz z obu stron nierówności należy odjąć (1 + x). Okazuje się, że: 2x - 4 - (1 + x)> 0. Po otwarciu nawiasów i podaniu takich warunków nierówność przyjmuje postać: x - 5> 0.
Porównując ją do zera, łatwo jest znaleźć rozwiązanie: x = 5.
Teraz ten punkt z numerem 5 musisz zaznaczyć na belce współrzędnych. Następnie sprawdź znaki oryginalnej funkcji. W pierwszym przedziale od minus nieskończoności do 5 można przyjąć liczbę 0 i zastąpić ją nierównością wynikającą z przekształceń. Po obliczeniach okazuje się, że -7> 0. pod łukiem interwału musisz podpisać znak minus.
W następnym przedziale od 5 do nieskończoności możesz wybrać liczbę 6. Następnie okazuje się, że 1> 0. Pod łukiem znak "+" jest podpisany. Ten drugi interwał będzie odpowiedzią na nierówność.
Odpowiedź: x leży w przedziale (5; ∞).
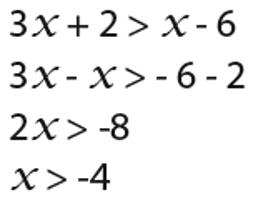
Drugi przykład. Wymagane jest rozwiązanie układu dwóch równań: 3x + 3 ≤ 2x + 1 i 3x - 2 ≤ 4x + 2.
Decyzja. LDL tych nierówności leży również w domenie dowolnych liczb, ponieważ podano funkcje liniowe.
Następnie musisz postępować etapami. Najpierw przekonwertuj pierwszą z nierówności i zrównaj ją do zera. 3x + 3 - 2x - 1 = 0. To jest x + 2 = 0. Zatem x to -2.
Druga nierówność przyjmie postać takiego równania: 3x - 2 - 4x - 2 = 0. Po transformacji: -x - 4 = 0. Daje wartość dla zmiennej równej -4.
Te dwie liczby powinny być zaznaczone na osi, przedstawiające przedziały. Ponieważ nierówność nie jest ścisła, wszystkie punkty muszą zostać zamalowane. Pierwszy interwał od minus nieskończoności do -4. Niech liczba będzie -5. Pierwsza nierówność da wartość -3, a druga, co oznacza, że ta luka nie jest zawarta w odpowiedzi.
Drugi przedział to od -4 do -2. Możesz wybrać liczbę -3 i zastąpić ją w obu nierównościach. W pierwszym i drugim uzyskuje się wartość -1. Pod łukiem "-".
W ostatnim przedziale od -2 do nieskończoności najlepszą liczbą jest zero. Konieczne jest zastąpienie go i znalezienie wartości nierówności. W pierwszym z nich uzyskuje się liczbę dodatnią, a drugą - zero. Ta luka powinna być również wykluczona z odpowiedzi.
Z trzech przedziałów rozwiązanie nierówności jest tylko jedno.
Odpowiedź: x należy do [-4; -2].

Trzeci przykład. | 1 - x | > 2 | x - 1 |.
Decyzja. Pierwszym krokiem jest określenie punktów, w których funkcje znikają. Po lewej stronie liczba ta będzie wynosić 2, dla prawej - 1. powinny być zaznaczone na promieniu i określić odstępy między znakami stałości.
W pierwszym przedziale, od minus nieskończoności do 1, funkcja z lewej strony nierówności przyjmuje wartości dodatnie, a od prawej przyjmuje wartości ujemne. Pod łukiem musisz zapisać dwie litery "+" i "-" obok siebie.
Następny interwał to od 1 do 2. Na nim obie funkcje przyjmują wartości dodatnie. Pod łukiem dwa plusy.
Trzeci interwał od 2 do nieskończoności daje następujący wynik: lewa funkcja jest ujemna, prawa - dodatnia.
Biorąc pod uwagę powstałe znaki, konieczne jest obliczenie wartości nierówności dla wszystkich przedziałów.
Na pierwszym, otrzymujemy następującą nierówność: 2 - x> - 2 (x - 1). Wartość ujemna przed dwoma w drugiej nierówności wynika z faktu, że funkcja ta jest ujemna.
Po transformacji nierówność wygląda następująco: x> 0. Natychmiast podaje wartości zmiennej. Oznacza to, że z tego przedziału wróci tylko przedział od 0 do 1.
Na drugim: 2 - x> 2 (x - 1). Konwersje dadzą następującą nierówność: -3x + 4 więcej niż zero. Jego zero to x = 4/3. Biorąc pod uwagę znak nierówności okazuje się, że x musi być mniejsze od tej liczby. Dlatego interwał ten jest zredukowany do przedziału od 1 do 4/3.
Ten ostatni podaje następujący zapis nierówności: - (2 - x)> 2 (x - 1). Jego transformacja prowadzi do: x> 0. To znaczy, że równanie jest prawdziwe dla x mniej niż zero. Oznacza to, że w wymaganej nierówności luki nie daje rozwiązań.
W pierwszych dwóch odstępach granica okazała się numerem 1. Należy ją sprawdzić osobno. Oznacza to zastąpienie pierwotnej nierówności. Okazuje się: | 2 - 1 | > 2 | 1 - 1 |. Obliczenia dają, że 1 jest większe niż 0. Jest to poprawna instrukcja, więc jedna jest zawarta w odpowiedzi.
Odpowiedź: x leży w przedziale (0; 4/3).