Dwusieczna trójkąta - co to jest?

Geometria jest jedną z najbardziej złożonych i skomplikowanych nauk. W tym, co wydaje się oczywiste na pierwszy rzut oka, bardzo rzadko okazuje się poprawne. Bisektery, wysokości, mediany, projekcje, styczne to ogromna liczba naprawdę trudnych terminów, z którymi bardzo łatwo się zdezorientować.

W rzeczywistości, przy odpowiednim pragnieniu, można zrozumieć teorię dowolnej złożoności. Jeśli chodzi o dwusieczną, medianę i wzrost, musisz zrozumieć, że nie są one charakterystyczne dla trójkątów. Na pierwszy rzut oka są to proste linie, ale każda z nich ma swoje właściwości i funkcje, których znajomość znacznie upraszcza rozwiązywanie problemów geometrycznych. Czym jest dwusieczna trójkąta?

Definicja

Termin "dwusieczna" pochodzi od kombinacji łacińskich słów "dwa" i "wyciąć", "wyciąć", co pośrednio wskazuje na jego właściwości. Zazwyczaj, gdy dzieci są wprowadzane do tej wiązki, proszone są o zapamiętanie krótkiej frazy: "Dwusieczna jest szczurem biegnącym w rogach i o połowę kąta". Oczywiście, takie wyjaśnienie nie jest odpowiednie dla starszych uczniów, poza tym zazwyczaj nie pyta się o węgiel, ale o to geometryczny kształt. Zatem dwusieczną trójkąta jest promień, który łączy wierzchołek trójkąta z przeciwną stroną, dzieląc ten kąt na dwie równe części. Punkt przeciwnej strony, do której dochodzi dwusieczna, dla arbitralnego trójkąta wybierany jest losowo.

Podstawowe funkcje i właściwości

Główne właściwości tej wiązki trochę. Po pierwsze, ponieważ dwusieczna trójkąta dzieli kąt na pół, każdy punkt leżący na nim będzie znajdował się w jednakowej odległości od boków tworzących wierzchołek. Po drugie, w każdym trójkącie można narysować trzy biseksety, zależnie od liczby dostępnych kątów (dlatego już cztery będą w tym samym czworoboku, i tak dalej). Punkt, w którym przecinają się wszystkie trzy promienie, jest środkiem okręgu wpisanego w trójkąt.

Właściwości są skomplikowane

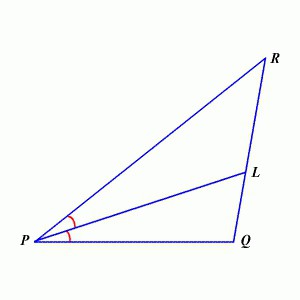
Komplikujmy trochę teorię. Inna interesująca właściwość: dwusieczna kąta trójkąta dzieli przeciwną stronę na segmenty, których stosunek jest równy stosunkowi boków tworzących wierzchołek. Na pierwszy rzut oka jest to trudne, ale w rzeczywistości wszystko jest proste: na proponowanej figurze RL: LQ = PR: PK. By the way, właściwość ta została nazwana twierdzeniem o Bisectrix i po raz pierwszy pojawiła się w pracach starożytnego greckiego matematyka Euklidesa. Przypomnieli sobie je w jednym z rosyjskich podręczników dopiero w pierwszej ćwierci siedemnastego wieku.

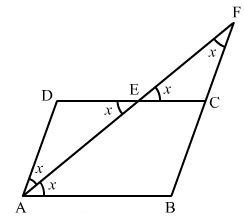
Trochę trudniejsze. W czworokącie dwusieczna odcina trójkąt równoramienny. Ta figura pokazuje wszystkie równe kąty dla mediany AF.

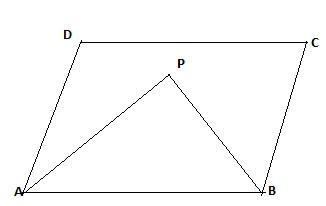
Ponadto w czworobokach i trapezach dwusieczne jednostronnych kątów są prostopadłe do siebie. Na rysunku kąt APB wynosi 90 stopni.

W trójkącie równoramiennym

Trójkąt równoramienny jest znacznie bardziej użytecznym promieniem. Jednocześnie jest to nie tylko dzielnik kąta na pół, ale także mediana i wysokość.

Mediana to odcinek, który wychodzi z pewnego kąta i pada na środek przeciwnej strony, dzieląc go na równe części. Wysokość jest prostopadła, spadła z wierzchołka na przeciwną stronę, a jej pomoc można zredukować do prostego i prymitywnego twierdzenia Pitagorasa. W tej sytuacji dwusieczna trójkąta jest równa pierwiastkowi różnicy między kwadratem przeciwprostokątnej a drugim odgałęzieniem. By the way, jest to właściwość, która jest najczęściej spotykana w problemach geometrycznych.

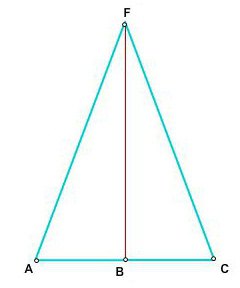
Aby naprawić: w tym trójkącie dwusieczna FB jest medianą (AB = BC) i wysokością (kąty FBC i FBA są 90 stopni).

Ogólnie

Co więc musisz zapamiętać? Dwusieczna trójkąta to promień, który dzieli jego szczyt na pół. Na przecięciu trzech promieni znajduje się środek koła wpisany w ten trójkąt (jedyną wadą tej właściwości jest to, że nie ma ona wartości praktycznej i służy jedynie do prawidłowego wykonania rysunku). Dzieli on również przeciwną stronę na segmenty, których stosunek jest równy stosunkowi boków, pomiędzy którymi ten promień przeszedł. W kształcie czworoboku, właściwości są nieco bardziej skomplikowane, ale, aby przyznać, praktycznie nie występują one w zadaniach na poziomie szkoły, a zatem zazwyczaj nie są dotknięte przez program.

Dwusieczna trójkąta równoramiennego jest ostatecznym marzeniem każdego ucznia. Jest to jednocześnie mediana (czyli dzieli przeciwną stronę na pół) i wysokość (prostopadle do tej strony). Rozwiązywanie problemów z takim dwusiecznym jest zredukowane do twierdzenia Pitagorasa.

Znajomość podstawowych funkcji dwusiecznej, a także jej podstawowe właściwości, jest niezbędna do rozwiązywania problemów geometrycznych o średnim i wysokim stopniu złożoności. W rzeczywistości promień ten znajduje się tylko w planimetrii, więc nie można powiedzieć, że zapamiętywanie informacji na jego temat pozwoli poradzić sobie ze wszystkimi rodzajami zadań.