Pojęcie momentu pędu, jego prawo zachowania i przykład rozwiązania problemu

Ruch obrotowy jest nie mniej powszechny niż ruch liniowy obiektów. Aby to zweryfikować, wystarczy przypomnieć obrót kół samochodów i rowerów, ostrza śmigłowców i wentylatorów, planety wokół własnej osi i wokół gwiazd. Aby opisać proces ruchu kołowego obiektów, używana jest wielkość fizyczna określana jako "moment pędu". Rozważ w artykule, co to jest.

Moment pędu cząstki i oś obrotu

Poniżej znajduje się rysunek, który schematycznie pokazuje, że cząstka lub punkt masy materialnej m porusza się wzdłuż kołowej trajektorii o promieniu ¯ z prędkością ν skierowaną stycznie. Oś obrotu jest prostopadła do płaszczyzny figury w punkcie O.

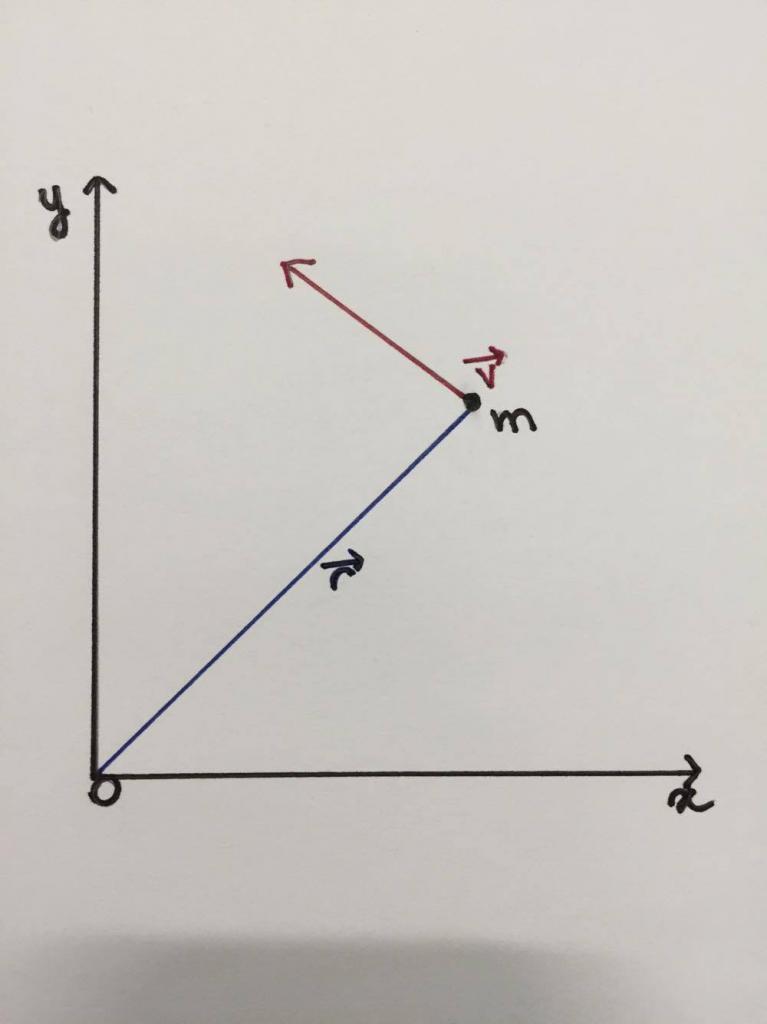
Wprowadzamy następującą ilość fizyczną:

L¯ = r¯ * m * v¯ = r¯ * p¯.

Nazywa się to momentem pędu lub pędem kątowym. Jak widać, jest to wielkość wektorowa. Jego kierunek można określić za pomocą zasady prawej ręki: musisz skierować 4 palce, aby poruszając się po wektorze r¯, dotarły do ​​końca wektora p¯ (lub v¯), a kciuk pokaże kierunek L¯. W tym przypadku L¯ jest skierowany do czytnika prostopadle do płaszczyzny rysunku.

Ponieważ prędkość cząstki (pędu) na rysunku jest skierowana pod kątem prostym do wektora ¯, zredukowane równanie można przepisać w postaci skalarnej:

L = r * m * v = r * p.

Prędkość kątowa i moment bezwładności

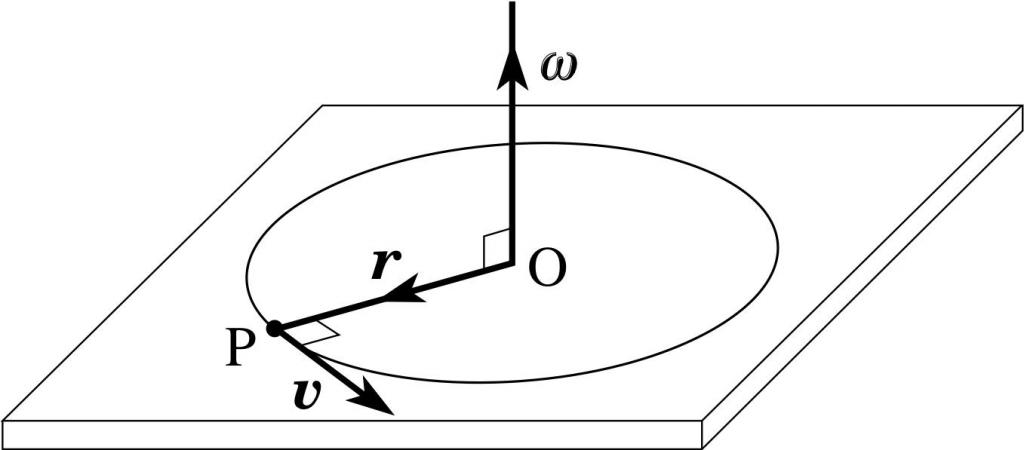
Pęd cząstki z poprzedniego przykładu można zapisać przez prędkość kątową ω. Aby to zrobić, używamy jego połączenia z prędkością liniową:

ω = v / r => v = ω * r.

Wstawiając ostatnie równanie na równanie skalarne dla L, otrzymujemy:

L = r ² * m * ω = I * ω, gdzie I = r ² * m.

Tutaj jestem momentem bezwładności cząstki. Uzyskane wyrażenie jest często wykorzystywane do rozwiązywania praktycznych problemów, z których jeden zostanie omówiony poniżej.

Prawo zachowania ruchu obrotowego

Ruch w okręgu, a także ruch liniowy obiektów w przestrzeni, charakteryzuje się prawami zachowania. Jednym z nich jest zachowanie momentu pędu. Otrzymujemy to prawo.

Równanie rozpatrywanego rodzaju ruchu ma następującą formę:

dL / dt = M.

Gdzie dL / dt charakteryzuje zmianę momentu pędu ciała w czasie, gdy wpływa na niego pewien moment M wytworzony przez siły zewnętrzne (nie wewnętrzne). Jeśli ten moment siły wynosi zero, wówczas lewa strona wyrażenia znika, co oznacza L = const. W tym przypadku możemy napisać następującą równość:

L = const = I ₁ * ω ₁ = I ₂ * ω ₂ .

Co oznacza ta płyta? Mówi się, że jeśli jakieś ciało obróciło się z prędkością ω ₁ i miał moment bezwładności I ₁ , to z powodu pewnych sił wewnętrznych (nie zewnętrznych) moment bezwładności zmienił się i stał się równy I ₂ , wtedy nowa prędkość obrotowa ω ₂ będzie proporcjonalna związane z tą zmianą.

Zapisaną relację nazywa się prawem zachowania pędu kątowego punktu (ciała) przez analogię z odpowiednim prawem dla wielkości liniowych (zachowanie pędu), ponieważ moment bezwładności pełnią rolę masy, a wartość kątowa ω odgrywa rolę masy.

Korzystanie z prawa L = const

Relację rozważaną w poprzednim paragrafie widać w działaniu, gdy wykonują je łyżwiarze lub baletnice. Wykonując skomplikowane akrobacje, obracają swoje ciała, rozpraszają ręce i nogi, a następnie przyciskają swoje kończyny do ciała. Ta ostatnia czynność prowadzi do zmniejszenia wartości I, a zatem do zwiększenia prędkości obrotowej, co daje dość spektakularny efekt.

Innym przykładem zastosowania niezmienności momentu pędu układu jest realizacja obrotu sztucznego satelity w przestrzeni. Aby to zrobić, należy uruchomić specjalne koło zamachowe. Ponieważ całkowity moment pędu nie powinien ulec zmianie z powodu działania sił wewnętrznych, sam satelita zaczyna się obracać w przeciwnym kierunku. Gdy tylko obraca się do pożądanego kąta wokół osi, koło zamachowe zatrzymuje się za pomocą silnika elektrycznego, a korpus satelity również zatrzymuje jego obrót.

Oblicz moment bezwładności

Ponieważ wartość I jest obecna w prawie zachowania ruchu kołowego, powinniśmy powiedzieć o tym kilka słów. Charakteryzuje bezwładność systemu, czyli "trudność" lub "łatwość" uwolnienia go. Na przykład koło zamachowe samochodu ma dużą masę i stosunkowo duży promień, więc jego moment bezwładności jest znaczny. Wręcz przeciwnie, koło rowerowe jest wykonane z aluminiowej obręczy lekkiej, więc do tego będę względnie mały.

Aby obliczyć tę cechę fizyczną, użyj wzoru:

I = ∫ _m (r ² * dm).

Stąd widać, że moment bezwładności jest cechą systemu, do którego wchodzi ciało rewolucji, a nie samym ciałem. Fakt ten odróżnia I od inercji liniowej, która zależy wyłącznie od właściwości ciała (jego masy).

Zadanie z obracającym się prętem

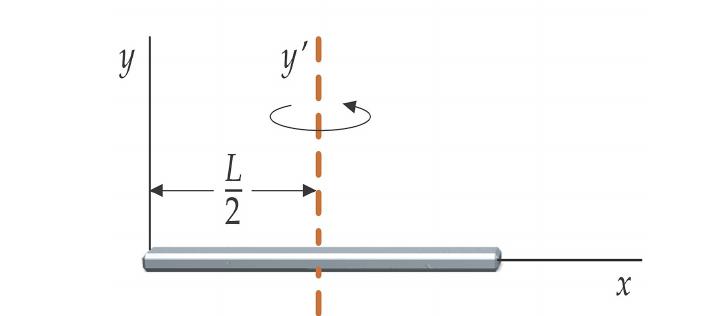
Rozwiążemy interesujący problem: jest solidny pręt, który obraca się wokół osi znajdującej się na jej końcu. Jeśli ta oś zostanie płynnie przesunięta do środka masy pręta, jak zmieni się jego prędkość obrotowa?

Jest to klasyczne zadanie zastosowania prawa zachowania momentu pędu. Trudność polega na obliczeniu zmiany momentu bezwładności. Aby to zrobić, możesz użyć powyższej formuły z całką, ale łatwiej będzie przyjrzeć się wymaganym wartościom I w literaturze.

Na początku oś obrotu przechodziła przez koniec pręta. W przypadku tego układu moment bezwładności jest równy:

I ₁ = m * L 2/3, gdzie L jest długością pręta, m jest jego masą.

Gdy oś została przesunięta do środka masy obiektu, zmienił się moment bezwładności, stał się równy:

I ₂ = m * L 2/12.

Zastosuj prawo zachowania dla L, otrzymamy:

m * L 2/3 * ω ₁ = m * L 2/12 * ω ₂ => ω ₂ / ω ₁ = m * L 2/3 / (m * L 2/12) = 4.

Otrzymaliśmy odpowiedź na problem: pręt obraca się 4 razy szybciej niż na początku.