Powierzchnia pryzmatu. Obszar podstawy i powierzchni bocznej. Podstawa trójkątnego pryzmatu

W geometrii przestrzennej, przy rozwiązywaniu problemów z pryzmatami, często występuje problem z obliczaniem obszaru boków lub ścian, które tworzą te trójwymiarowe kształty. Artykuł poświęcony jest zagadnieniu powierzchni podstawy pryzmatu i jego powierzchni bocznej.

Postać pryzmatu

Przed przystąpieniem do rozpatrywania wzorów dotyczących powierzchni podstawy i powierzchni pryzmy tego czy innego rodzaju, należy ustalić, o którą z nich chodzi.

Pryzmat w geometrii jest postacią przestrzenną składającą się z dwóch równoległych wielokątów, które są równe i kilku czworokątów lub równoległoboków. Liczba tych ostatnich jest zawsze równa liczbie wierzchołków pojedynczego wielokąta. Na przykład, jeśli liczba jest tworzona przez dwa równoległe n-gony, liczba równoległoboków będzie równa n.

Równoległobok łączący n-gony nazywa się bokami pryzmatu, a ich całkowity obszar jest obszarem powierzchni bocznej figury. Same n-gony nazywane są zasadami.

Powyższy rysunek pokazuje przykład pryzmy wykonanej z papieru. Żółty prostokąt jest jego podstawą. Na drugim stoi ta sama podstawa. Czerwone i zielone prostokąty są bocznymi ścianami.

Jakie są pryzmaty?

Istnieje kilka rodzajów pryzmatów. Wszystkie różnią się od siebie tylko dwoma parametrami:

• typ n-gon, tworząc podstawę;
• kąt między n-gonem a bokami.

Na przykład, jeśli podstawami są trójkąty, wówczas pryzmat nazywany jest trójkątnym, jeśli czworokąty, jak na poprzedniej figurze, figurę nazywa się czworobocznym pryzmatem i tak dalej. Dodatkowo, n-gon może być wypukły lub wklęsły, wówczas ta właściwość jest również dodawana do nazwy pryzmatu.

Kąt między powierzchniami bocznymi a podstawą może być prosty, ostry lub tępy. W pierwszym przypadku mówią o prostokątnym pryzmacie, w drugim - o nachyleniu lub ukośnym.

W specjalnym typie liczb przypisz właściwy pryzmat. Mają najwyższą symetrię wśród innych pryzmatów. Będzie to poprawne tylko jeśli jest prostokątne, a jego podstawa jest regularna n-gon. Poniższy rysunek pokazuje zestaw prawidłowych graniastosłupów, w których liczba boków n-gona zmienia się od trzech do ośmiu.

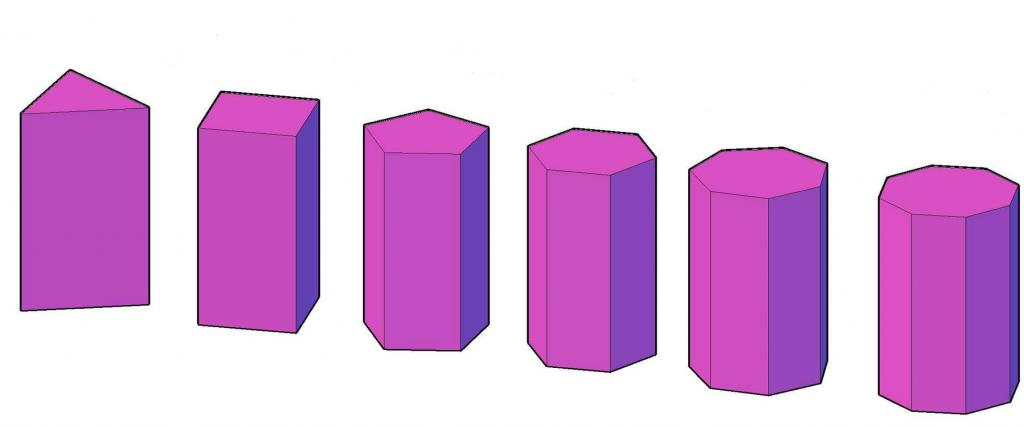
Powierzchnia pryzmatu

Pod powierzchnią rozpatrywanych postaci dowolnego typu rozumiemy wszystkie punkty, które należą do powierzchni pryzmatu. Powierzchnia pryzmy jest wygodna do zbadania, biorąc pod uwagę jej rozwój. Poniżej znajduje się przykład takiego przemiatania dla trójkątnego pryzmatu.

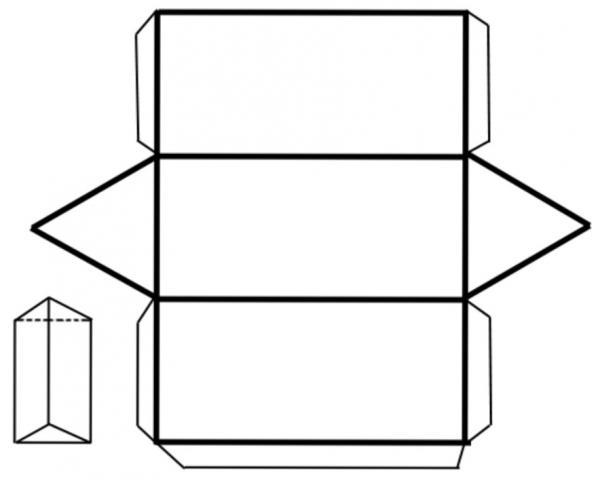
Widać, że cała powierzchnia jest utworzona przez dwa trójkąty i trzy prostokąty.

W przypadku pryzmatu typu ogólnego jego powierzchnia będzie składać się z dwóch baz węglowych i n czworoboków.

Rozważmy bardziej szczegółowo kwestię obliczania powierzchni pryzmatów różnych typów.

Podstawa pryzmatu jest prawidłowa

Być może najprostszym zadaniem podczas pracy z pryzmatami jest problem ze znalezieniem obszaru podstawy właściwej figury. Ponieważ jest on utworzony przez n-gon, w którym wszystkie kąty i długości boków są takie same, zawsze można je podzielić na identyczne trójkąty, w których znane są kąty i boki. Całkowita powierzchnia trójkątów będzie powierzchnią n-gon.

Innym sposobem określenia części powierzchni pryzmatu (podstawy) jest użycie znanej formuły. Ma następującą postać:

S _n = n / 4 * a ² * ctg (pi / n)

To znaczy, obszar S _n n-gonu jest jednoznacznie określony na podstawie długości jego boku. Pewna trudność w obliczeniu przez formułę może być obliczeniem cotangensa, szczególnie gdy n> 4 (dla n≤4, wartości cotangens są danymi tabelarycznymi). Aby określić tę funkcję trygonometryczną, zaleca się użycie kalkulatora.

Podczas formułowania problemu geometrycznego należy zachować ostrożność, ponieważ może być konieczne znalezienie obszaru podstawy pryzmatu. Następnie wartość uzyskana za pomocą wzoru powinna zostać pomnożona przez dwa.

Podstawa trójkątnego pryzmatu

Korzystając z przykładu trójkątnego pryzmatu, zastanawiamy się, jak znaleźć obszar podstawy tej figury.

Po pierwsze, rozważ prosty przypadek - właściwy pryzmat. Obszar podstawy oblicza się za pomocą wzoru podanego w powyższym akapicie, należy zastąpić go n = 3. Otrzymujemy:

S ₃ = 3/4 * a ² * ctg (pi / 3) = 3/4 * a ² * 1 / √3 = √ 3/4 * a ²

Pozostaje zastąpić konkretne wartości długości a boku trójkąta równobocznego w wyrażeniu, aby uzyskać obszar jednej podstawy.

Teraz przypuśćmy, że istnieje pryzmat, którego podstawą jest arbitralny trójkąt. Znane są jego dwa boki a i b oraz kąt między nimi α. Ta liczba jest pokazana poniżej.

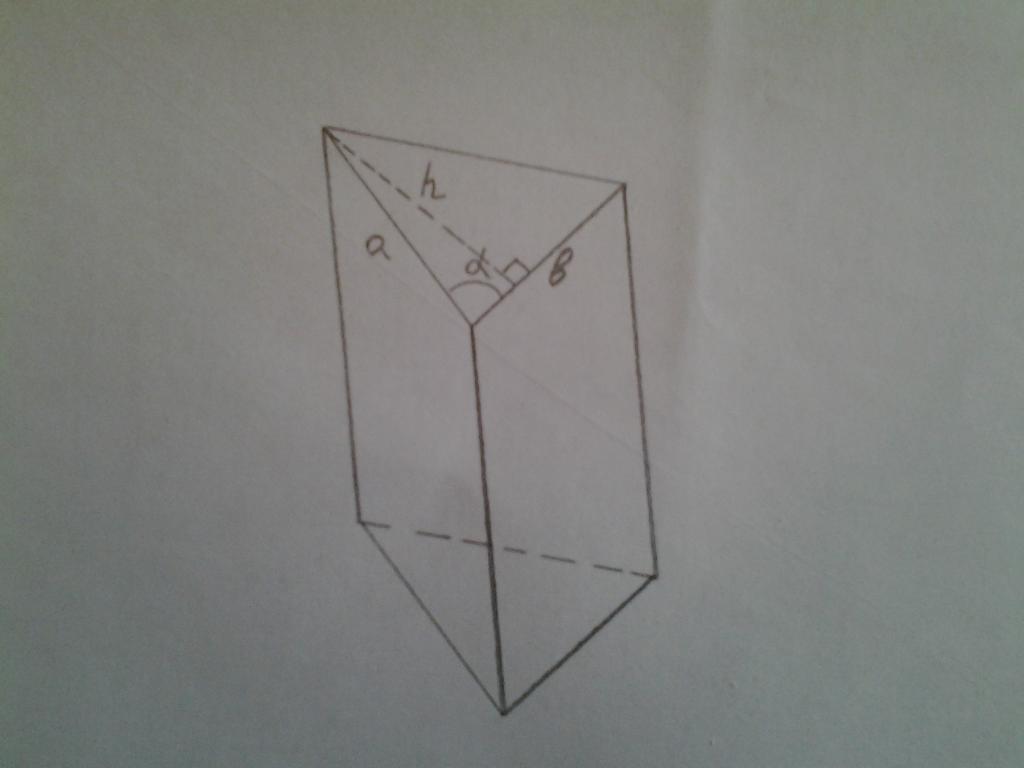
Jak w tym przypadku znaleźć powierzchnię podstawy trójkąta pryzmatycznego? Należy pamiętać, że powierzchnia dowolnego trójkąta jest równa połowie iloczynu boku i wysokości obniżonej po tej stronie. Rysunek pokazuje wysokość h do boku b. Długość h odpowiada iloczynowi sinusa kąta alfa i długości boku a. Następnie obszar całego trójkąta jest równy:

S = 1/2 * b * h = 1/2 * b * a * sin (α)

Jest to obszar podstawy przedstawionego trójkątnego pryzmatu.

Powierzchnia boczna

Ustaliliśmy, jak znaleźć obszar podstawy pryzmatu. Boczna powierzchnia tej figury zawsze składa się z równoległoboków. W przypadku pryzmatów bezpośrednich równoległoboki stają się prostokątami, więc ich łączna powierzchnia jest łatwa do obliczenia:

S = Σ _{i = 1} ⁿ (a _i * b)

Tutaj b jest długością krawędzi bocznej, a _i jest długością boku i-tego prostokąta, który pokrywa się z długością boku n-gon. W przypadku zwykłego pryzmatu n, otrzymujemy proste wyrażenie:

S = n * a * b

Jeśli pryzmat jest nachylony, to w celu określenia powierzchni jego powierzchni bocznej, wykonaj prostopadłe cięcie, obliczyć jego obwód P _sr i pomnożyć przez długość krawędzi bocznej.

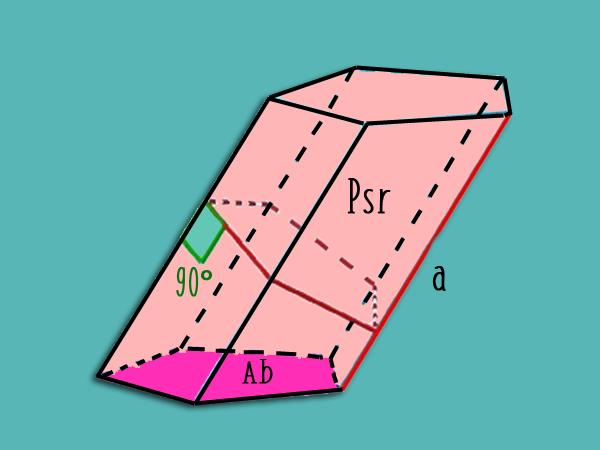
Powyższy rysunek pokazuje, jak wykonać ten kawałek na nachylonym pięciokątnym pryzmacie.