Wzór Ciołkowskiego: użycie i przykład
Formuła Konstantina Eduardowicza Ciołkowskiego wyraża maksymalną prędkość samolot, który dociera podczas lotu odrzutowego. Uzyskuje się ją poprzez integrację równania Meszerskiego.
Formuła Ciołkowski
Ta formuła wyraża prędkość rakiety przenoszonej przez gazy z spalonego paliwa. Równanie Meszerskiego i wzór Ciołkowskiego są ze sobą nierozerwalnie połączone - równanie Meszerskiego opisuje masę punktu materialnego, który zmienia się wraz z upływem czasu, podczas gdy ruch rakietowy stale zmniejsza swoją masę z powodu spalania paliwa. Zmiana prędkości ze zmienną masą (zmniejszającą się w naszym przypadku) ruchomego ciała - tak sugeruje napęd odrzutowy. Formuła Ciołkowskiego opiera się na tym.
Ad
Aby rozwiązać szereg problemów mechaniki teoretycznej w dziedzinie napędu odrzutowego, zastosowano równanie Meszerskiego (podstawowe równanie punktu materialnego o zmiennej masie) i wzór Ciołkowskiego (wzór ostatecznej prędkości samolotu), które nazywane są podstawowymi zależnościami teorii napędu odrzutowego.
Podstawą do projektowania i planowania w zakresie lotów kosmicznych jest właśnie formuła Ciołkowskiego, której zakończenie było prawdziwym przełomem w eksploracji kosmosu.
Zadania Ciołkowskiego
Aby rozwiązać problem lotów międzyplanetarnych, K. E. Ciołkowski uważał rakietę za środek lotu. Wyliczył on wzór, który można wykorzystać do określenia zależności masy statku powietrznego od paliwa i tempa rozdzielania produktów spalania rakiety stosowanej do paliwa w stosunku do niej. Pokazujemy dwa jego zadania:
Ad
- Badanie ruchu ciała o zmiennej masie z działającą na niego pojedynczą siłą reaktywną.
- Badanie ruchu ciała w jednolitym polu grawitacyjnym o zmiennej masie w pobliżu powierzchni Ziemi.
Słowo wstępne
Dla wszystkich lotów kosmicznych pierwotną i podstawową była formuła Ciołkowskiego dla prędkości rakiety, której wydajność jest przedstawiona poniżej.
Najpierw, z grubsza mówiąc, musisz wziąć to za punkt materialny. Siły grawitacji Ziemi i innych ciał niebieskich będą działać na nią (w momencie startu siła grawitacji Ziemi będzie oczywiście najsilniejsza), siła oporu powietrza z jednej strony i skierowana przeciwnie siła bierna wynikająca z uwolnienia spalonego gazu u podstawy ciała . Rakieta z dużą siłą wyrzuca te gazy, co oznacza przyspieszenie skierowane przeciwnie do strony emisji. Teraz musisz przedstawić te argumenty w postaci formuły.
Zasada lotu rakiety jest dość prosta. Z dużą prędkością gaz z rakiety jest wyciągany ze spalania paliwa, co daje samej rakiecie pewną siłę, która działa przeciwnie do kierunku ruchu. Ponieważ uważa się, że siły zewnętrzne nie działają na rakietę, system zostanie zamknięty, a jego pęd nie zależy od czasu.
Równanie Meshchersky'ego
Jednym z głównych przykładów ruchów ciała o różnej masie jest rakieta z pojedynczym stopniem, którego masa zmienia się tylko z powodu spalania zawartego w niej paliwa. Masa takiej rakiety składa się z niezmienionej (samej rakiety i jej ładunku) i zmiennej (paliwo). Taki przykład to uproszczony model.
Ad
Jednak w nowoczesnej produkcji rakiet stosowane są wielostopniowe rakiety. Zasada ich pracy polega na tym, że ze względu na dużą liczbę kroków są w stanie transportować i zużywać znacznie większą ilość paliwa po starcie. Po jego spaleniu rakieta otrzymuje znaczący impuls (znacznie większy niż ten, który można osiągnąć za pomocą jednego etapu), a części, które stały się niepotrzebne, są odłączane od podstawy, zmniejszając całkowitą wagę o 80-90%. Jednakże, aby obliczyć parametry wielostopniowej rakiety, należy zsumować wskaźniki każdego z jej składników.
Równanie różniczkowe Meszerskiego opisuje ruch punkt materialny o zmiennej masie.
(m + dm) (υ + dυ) + dm 'υ' - mυ = Fdt - w czasie dt (różnica między siłą w czasie t i dt + t będzie inkrementem).
Gdzie m i υ zależy od czasu, dt - pewien czas lotu. Powstaje bowiem siła ruchu gazu - dm 'υ', dm '- masa gazu powstającego z paliwa. F jest siłą wypadkową.
W powyższym wyrażeniu przyrost masy rakiety i gazu oraz prędkość pędzą do zera, więc wyrażenie przyjmuje następującą postać:
mdυ = υ''dm + Fdt,
ponadto, υ "równa się różnicy między prędkością gazu a prędkością i jest prędkością wypływu gazu.
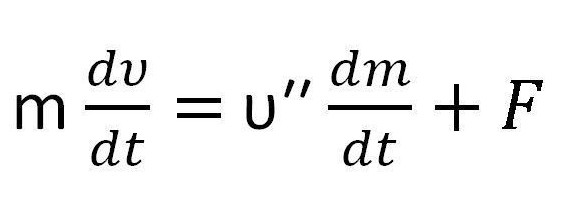 - równanie w formie zaczyna się zbiegać z drugim prawem Newtona - F = ma = m
- równanie w formie zaczyna się zbiegać z drugim prawem Newtona - F = ma = m
Nazywa się to równaniem Meszerskiego.
Wyprowadzenie wzoru Ciołkowskiego
Konieczne jest wyprowadzenie wzoru opisującego ruch ciała o zmiennej masie. Formuła Ciołkowskiego taka jest. Dane wyjściowe przedstawiono poniżej.
W tych obliczeniach zakłada się, że siły zewnętrzne nie działają na ruchome ciało, to znaczy F = 0.
Następnie mdυ = υ''dm
Ponieważ wpływ sił zewnętrznych na latającą rakietę wynosi zero, porusza się ona w linii prostej, a prędkość ruchu jest przeciwna do prędkości gazu. W związku z tym υ = -υ '
Ad
Okazuje się, że wyrażenie musi zostać zintegrowane.
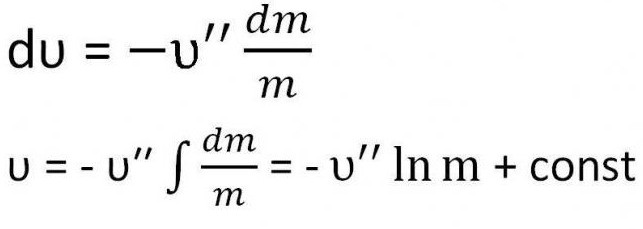
Konieczne jest znalezienie stałej. Aby to zrobić, wystarczy podstawić warunki początkowe do równania - prędkość wynosi zero, a masa jest sumą masy paliwa i masy rakiety (m 0 + m)
Ogólnie rzecz biorąc, m w formule składa się z dwóch parametrów - z ładowności i konstrukcji rakiety. Ładunek jest całkowitą wagą ładunku i załogi.
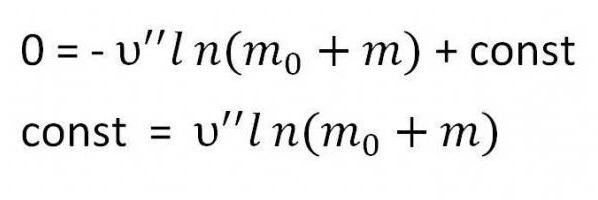
Zastępujemy znalezioną stałą w formule. W rezultacie uzyskuje się ekspresję wymaganej formuły.
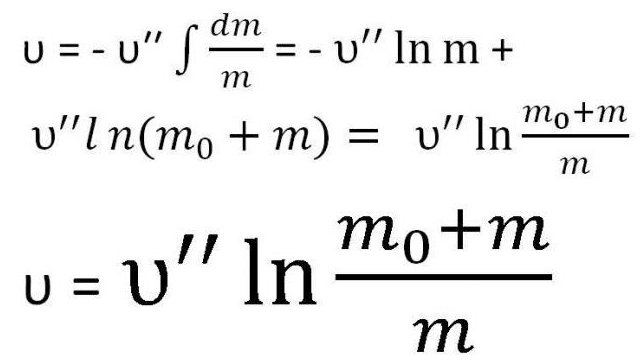
Jest to jedna z odmian formuły Ciołkowskiego dla prędkości. Czasami jednak konieczne jest dokładne uwzględnienie masy. Dlatego czasami jest napisane w następujący sposób:
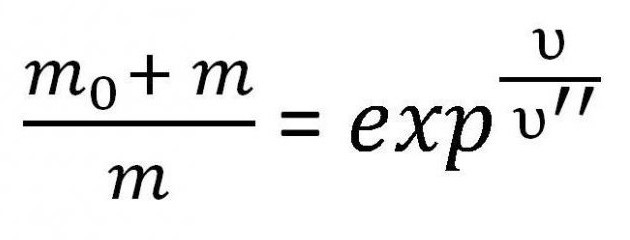
Ta formuła służy do obliczenia masy paliwa, która jest wymagana do opracowania określonej prędkości w określonych warunkach.
Rozważę dalej małe zadanie. Przypuśćmy, że rakieta musi rozwinąć pierwszą prędkość kosmiczną do obrotu wzdłuż orbity Ziemi. Wtedy najpierw musisz obliczyć masę oczywiście paliwo. Wtedy bardzo łatwo jest wyrazić to z formuły Ciołkowskiego.
Ad
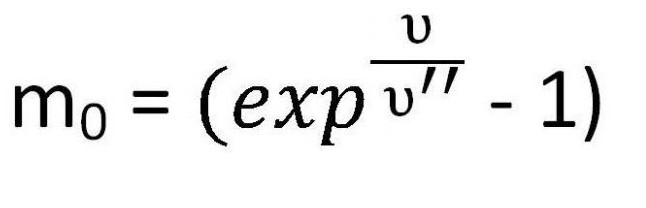
Mechanizmy relatywistyczne
Wszystkie powyższe formuły można stosować tylko w przypadku, gdy prędkość rakiety jest znacznie mniejsza niż prędkość światła (υ < Jednakże, jeśli prędkość rakiety można porównać do prędkości światła, konieczne jest zastosowanie innych praw. Niech m i υ będą masą rakiety w stanie i jej prędkością w dowolnym momencie t, a υ 'i m' będą prędkością uwalniania gazu i jego masą w tym samym czasie. Oznacza to, że m 'jest masą uwolnionego gazu, więc jego wartość do obliczeń jest nieistotna, m' = 0. Konieczne jest napisanie prawa zachowania pędu i prawa zachowania energii w mechanice relatywistycznej, a następnie rozróżnienie pierwszego równania, biorąc pod uwagę, że m '= 0 i otrzymamy wyrażenie trzecie. gdzie u jest wskaźnik emisji gazów. W oparciu o prawo dodawania prędkości w mechanice relatywistycznej, wyrażenie to następuje. Musi zostać przekonwertowany na υ 'i zintegrowany, aby uzyskać ostateczną wersję równania. A potem otrzymujemy wzór Ciołkowskiego na prędkość, porównywalną do prędkości światła. Można to również nazwać relatywistyczną formułą Ciołkowskiego. Możesz nieco komplikować zadanie i rozważyć jako przykład rakietę z kilkoma etapami. Tak więc, formuła Ciołkowskiego dla wielostopniowej rakiety jest sumą parametrów niezbędnych do obliczeń. Oznacza to, że w celu obliczenia prędkości dla wielostopniowej rakiety należy zsumować prędkość każdej z części składowych. Podstawą wszystkich lotów kosmicznych jest formuła Ciołkowskiego. Podczas obliczania lotu ważne jest, aby jasno zrozumieć, jaki procent energii uzyskanej po spaleniu paliwa jest wykorzystywany jako praca użyteczna? Tak więc wydajność nazywa się stosunkiem energie kinetyczne rakiety i gazy po wyrzuceniu. Oznacz m i m 'dla masy rakiety na początku i na końcu lotu, ciągły czas t. Odpowiednio, - szybkość wyrzucania gazów. Następnie, zgodnie ze wzorem Ciołkowskiego, wydajność silnika rakietowego można znaleźć w następujący sposób: Należy zauważyć, że ta wydajność jest bardzo mała i nie przekracza 5%, ponadto, podobnie jak w silnikach cieplnych, wskaźnik ten wynosi 80%. Niektóre zasoby używają nieco innej formuły Tsiolkovsky'ego, równania, w którym stosuje się inny parametr zamiast υ-I. W tym przypadku nazywam się specyficznym impulsem, a nawet wytłumaczeniem jest, że określony impuls jest wyrażany przez ciąg silnika i jego masowe spalanie paliwa w jednostce czasu. . Pierwsze pytanie, które przychodzi na myśl, to kwestia wymiarowości. W przeciwieństwie do prędkości, rozpęd ma inny wymiar, który zaprzecza istocie formuły. Jednak sam impuls właściwy pokrywa się z prędkością. Specyficzny impuls wskazuje liczbę sekund, w których silnik, wydając jednostkę paliwa, otrzyma jednostkę siły. Używane wyłącznie w opisie silnika odrzutowego. Formuła Ciołkowskiego dla wielostopniowej rakiety służy również do projektowania rakiety. W tym celu stosuje się całkowicie logiczną zależność, która jest praktycznie wprost proporcjonalna - im więcej paliwa zużywa się podczas lotu, tym większa będzie masa samej rakiety. Wynika to z faktu, że do transportu dużych ilości paliwa wymagane są odpowiednio duże zbiorniki, w związku z czym zwiększa się rozmiar statku, a nawet samego silnika. Pewnym rozwiązaniem tego problemu jest stosowanie paliw stałych, co wymaga mniejszych warunków przechowywania. Jednak w tym momencie ma najmniejszy konkretny impuls już istniejących. Formuła Ciołkowskiego jest również używana do obliczenia niezbędnej ilości paliwa dla rozwoju pewnej prędkości - zwykle jednej z czterech kosmicznych. 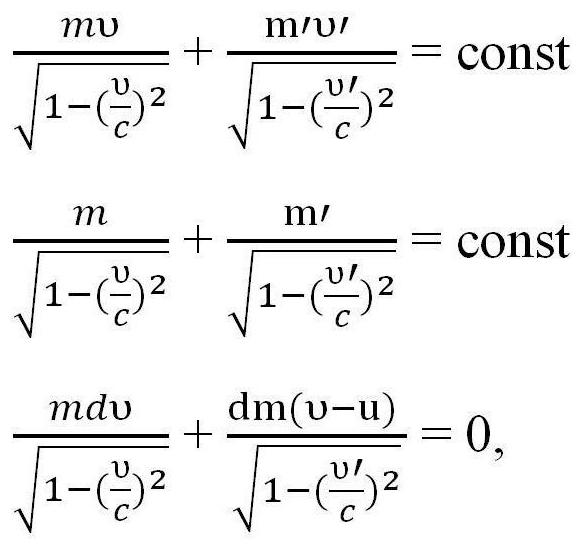
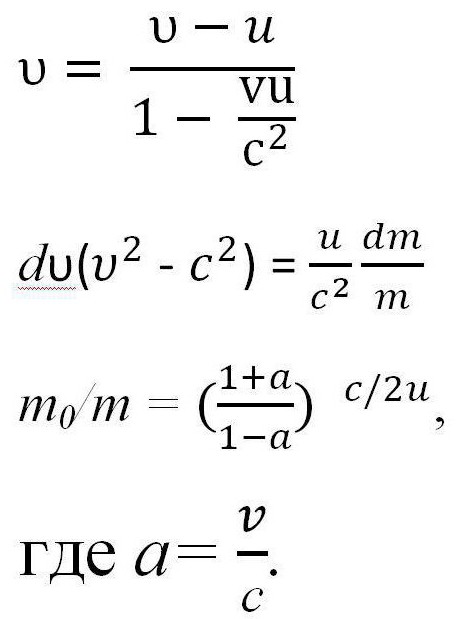
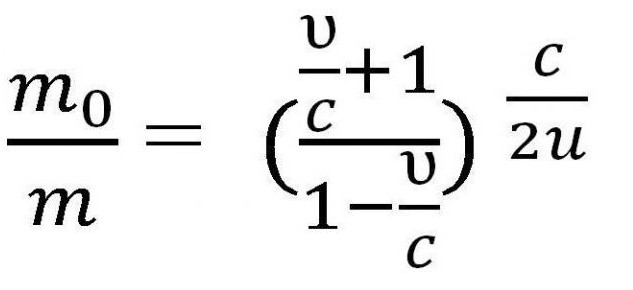
Kilka wniosków z formuły Ciołkowskiego
Wydajność rakiet
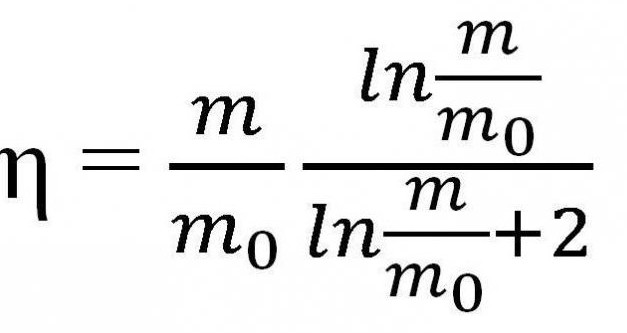
Inna forma formuły
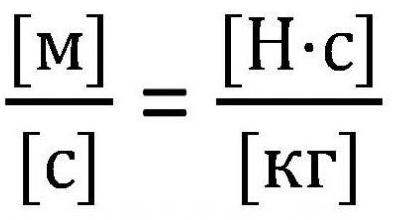
Użyj podczas tworzenia pocisków
Prędkości kosmiczne