Co to są liczby nieparzyste i jak je poznać?

Zanim powiemy o liczbach parzystych i nieparzystych, warto wyjaśnić kilka punktów, które grupy liczb są w ogóle. Jest to konieczne, aby nie próbować ustalić parzystości ułamka.

Jakie są liczby, aby rozpocząć naukę w szkole podstawowej?

Pierwsze są naturalne. Po raz pierwszy pojawili się również historycznie. Ludzkość potrzebowała policzyć przedmioty. Co więcej, gdy liczenie zera nie jest używane, więc nie jest zawarte w grupie liczb naturalnych. Tutaj wszystkie są liczbami całkowitymi, które są większe niż jeden.

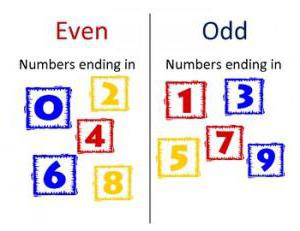
Dla nich najpierw podano definicję parzystości. Aby zrozumieć, która liczba jest dziwna, musisz pamiętać o znaku równości. Kończy się jedną z liczb: 0, 2, 4, 6, 8. Wszystkie pozostałe będą nieparzyste. Minimum z nich to jedno. Maksymalna nie istnieje.

Jakie liczby idą dalej?

Całość. Ich zestaw zawiera już zero i wszystkie liczby ujemne. Łańcuch liczb naturalnych ograniczał się do lewej, a po prawej ciągał się w nieskończoność. W liczbach całkowitych okazuje się być nieskończoną liczbą liczb i na lewo od zera.

W tym momencie definicja parzystości zmienia się nieznacznie. Teraz powinno być podzielone przez dwa bez reszty. Dlatego liczby nieparzyste podzielone przez dwa dają odpowiedź z resztą.

I nawet wpis ogólny jest wprowadzony: dla parzystego - 2n, nieparzystego - (2n + 1). Jeśli dla naturalnych nie ma tylko maksimum parzyste lub nieparzyste, to liczby całkowite nie mają minimum.

A co potem?

Liczby racjonalne (inna nazwa - prawdziwe). Oprócz tych już wymienionych, ten zestaw zawiera również ułamki. To znaczy liczby, które można przedstawić jako dwa. Pierwszym z nich jest licznik, który jest reprezentowany jako liczba całkowita. Drugi to mianownik, który nigdy nie jest zerowy.

Nawiasem mówiąc, pojęcie parytetu nie jest dla nich wprowadzone. Dlatego liczby nieparzyste zapisane jako ułamek w ogóle nie istnieją.

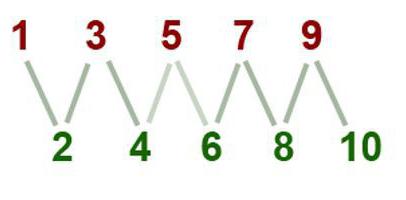
Jakie wyniki dają działania z liczbami parzystymi i nieparzystymi?

Można je rozpatrywać w kolejności rosnącej złożoności operacji arytmetycznej. Wtedy pierwszy i drugi będzie dodawanie i odejmowanie. Bez względu na to, który z nich zostanie wykonany, odpowiedź będzie zależeć tylko od początkowej pary liczb. Na przykład, jeśli początkowe liczby są równe, wynik działania zostanie podzielony przez dwa. Ten sam wynik będzie, jeśli istnieje różnica lub suma liczb nieparzystych. Aby uzyskać nieparzystą liczbę, musisz dodać lub odjąć nawet nieparzystą liczbę.

Można to łatwo zweryfikować za pomocą ich ogólnego zapisu. Na przykład dodanie dwóch liczb parzystych: 2n + 2n = 4n = 2 * 2n. Tutaj 2n jest liczbą parzystą, która jest nadal pomnożona przez dwa. Więc na pewno zostanie całkowicie podzielony na dwójkę. To znaczy, odpowiedź jest parzysta.

Przy dodawaniu parzystości do parzystości mamy następujący wpis: 2n + (2n + 1) = 4n + 1. Pierwsze wyrażenie jest liczbą parzystą, do której dodaje się jeden. Ostatni termin nie pozwoli podzielić tego wyniku na dwie części.

Trzecią czynnością jest mnożenie. Kiedy zostanie wykonany, zawsze będzie odpowiednia odpowiedź, jeśli istnieje co najmniej jeden czynnik równomierny. W sytuacji, gdy dwie liczby nieparzyste są mnożone razem, wynik będzie nieparzysty.

Aby zilustrować to ostatnie, należy wprowadzić następujący wpis: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Ponownie, pierwszy termin jest liczbą parzystą, a jednostka sprawi, że będzie nieparzysta.

Przy czwartym działaniu - podziale - wszystko nie jest tak jasne. Możesz zacząć od dwóch parzystych. Po pierwsze, ułamek może się okazać, a następnie parzystość nie jest pytaniem. Po drugie, wynikiem jest liczba całkowita. Ale nawet wtedy nie można uzyskać ostatecznej odpowiedzi na pytanie o przyszły parytet. Możesz ocenić to dopiero po podziale. Odpowiedź może być zarówno parzysta, jak i nieparzysta.

Jeśli liczba nieparzysta jest dzielona przez liczbę parzystą, odpowiedź jest zawsze ułamkowa. Dlatego jego parytet nie jest określony.

W przypadku podziału liczb nieparzystych wynik może być także ułamkiem. Ale jeśli odpowiedź jest całkowita, to z pewnością będzie dziwna.

Podczas dzielenia nawet przez nieparzyste, jak w poprzedniej sytuacji, istnieją dwie opcje: ułamek lub liczba całkowita. W drugim przypadku zawsze będzie równy.