Co to jest przyspieszenie? Rodzaje przyspieszenia. Formuły. Przykład rozwiązania problemu

Część fizyki odpowiedzialna za badanie cech ruchu w przestrzeni ciał nazywana jest kinematyką. W tym artykule rozważamy, jakie wielkości fizyczne w kinemacie są używane do opisu ruchu obiektów, a także ujawniają, czym jest przyspieszenie.

Ilości fizyczne w kinemacie

Kiedy ciało porusza się w przestrzeni, ważne jest, abyśmy wiedzieli, jaki dystans przebył w określonym czasie i wzdłuż którego trajektoria się porusza.

Aby opisać odległości przebywane w fizyce, stosowana jest koncepcja ścieżki - L. W przypadku ruchu po okręgu, zamiast ścieżki, stosowana jest koncepcja kąta obrotu θ. Wartość L w SI jest mierzona w metrach (m), a wartość θ jest mierzona w radianach (rad.).

Oprócz ścieżki ważne jest również poznanie prędkości ruchu ciał. Pod nim zrozumieć prędkość upływu odległości. Wyrażenie matematyczne dla prędkości liniowej przyjmuje postać:

v¯ = d L / dt

Aby opisać ruch w kole, zastosuj prędkość kątową ω, która jest obliczana w następujący sposób:

ω¯ = d θ / dt

Trzecią ważną wielkością kinematyki jest przyspieszenie.

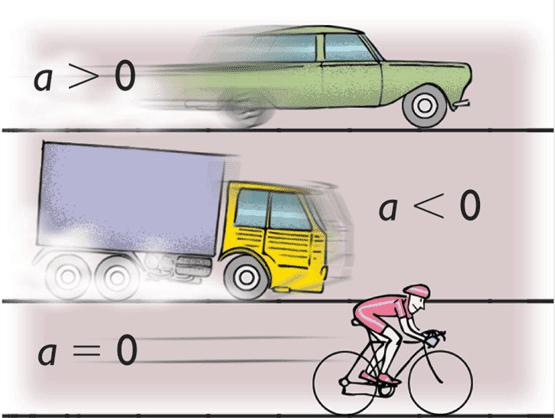
Co to jest przyspieszenie? Jest to ilość w fizyce, która pokazuje, jak szybko prędkość zmienia się w czasie. Matematycznie można to zapisać jako:

a¯ = d v¯ / dt

Jeśli zastąpimy wyrażenie dla prędkości w tej formule przyspieszenia, otrzymamy:

a = d ² L / dt ²

Przyspieszenie jest pierwszą pochodną prędkości względem czasu lub drugiej pochodnej w odniesieniu do czasu ścieżki zstępującej.

Styczne i normalne przyspieszenie

Powyżej podano definicję przyspieszenia. Nazywa się to kompletnym. W ogólnym przypadku kierunek pełnego przyspieszenia nie pokrywa się z kierunkiem wektora prędkości. Ten ostatni jest styczny do trajektorii ruchu w którymkolwiek z jego punktów.

Ponieważ prędkość jest wielkością wektorową, jej zmiana oznacza możliwość zmiany modułu i kierunku. W pierwszym przypadku mówią, że ciało ma przyspieszenie styczne, w drugim przypadku jest normalne.

Wzór na przyspieszenie styczne _t nie różni się od przyspieszenia pełnego a. Formuła ma postać:

a _t = dv / dt

To znaczy, styczne lub styczne, jak to się nazywa, przyspieszenie jest uzyskiwane z modułu prędkości w czasie. Wektor a _t ¯ pokrywa się z wektorem v ¯ z przyspieszonym ruchem i jest przeciwny do niego w zwolnionym tempie.

Normalne przyspieszenie jest wielkością fizyczną, która prowadzi do krzywizny prostoliniowej trajektorii poruszających się ciał. Jest on kierowany wzdłuż promienia krzywizny trajektorii, to jest normalny w stosunku do niego. Formuła jego definicji to:

a _c = v ² / r

Normalne przyspieszenie _c zależy od modułu prędkości v i promienia krzywizny trajektorii r. Oczywiście, w przypadku ruchu wzdłuż prostego promienia, r można uznać za równy nieskończoności. To ostatnie oznacza, że ​​normalne przyspieszenie wynosi zero dla ruchu prostoliniowego.

W przypadku ruchu kołowego wektor a _c ¯ jest kierowany do jego środka wzdłuż promienia. Z tego powodu wartość _c nazywana _jest również przyspieszeniem dośrodkowym.

Pełne przyspieszenie

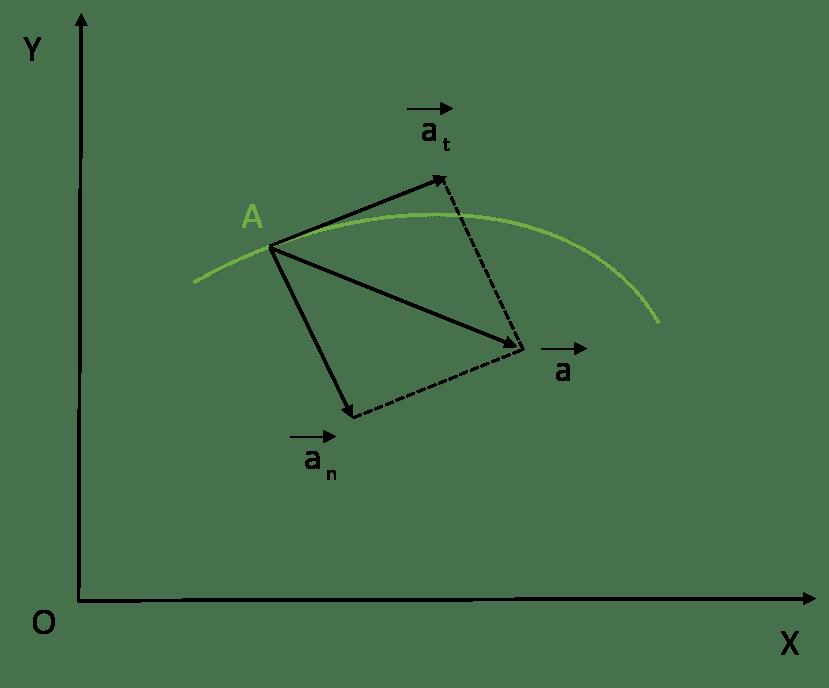
Całkowity wektor przyspieszenia jest zawsze sumą stycznych i normalnych składników. Ponieważ są one prostopadłe względem siebie, do obliczenia całkowitego modułu przyspieszenia można zastosować twierdzenie Pitagorasa. Pożądana formuła pełnego przyspieszenia ma postać:

a = √ (a _t ² + a _c ² )

Aby określić, gdzie skierowany jest wektor a¯, wystarczy obliczyć kąt między nim a jakimkolwiek komponentem. Na przykład kąt φ między wektorami ai _t jest równy:

φ = arctg (a _c / a _t )

Przypomnijmy, że przyspieszenie dośrodkowe jest niezerowe tylko wtedy, gdy krzywizna trajektorii różni się od nieskończoności. W przypadku ruchu prostoliniowego całkowite przyspieszenie w zakresie wielkości i kierunku jest równe składowi stycznym.

Przyspieszenie kątowe

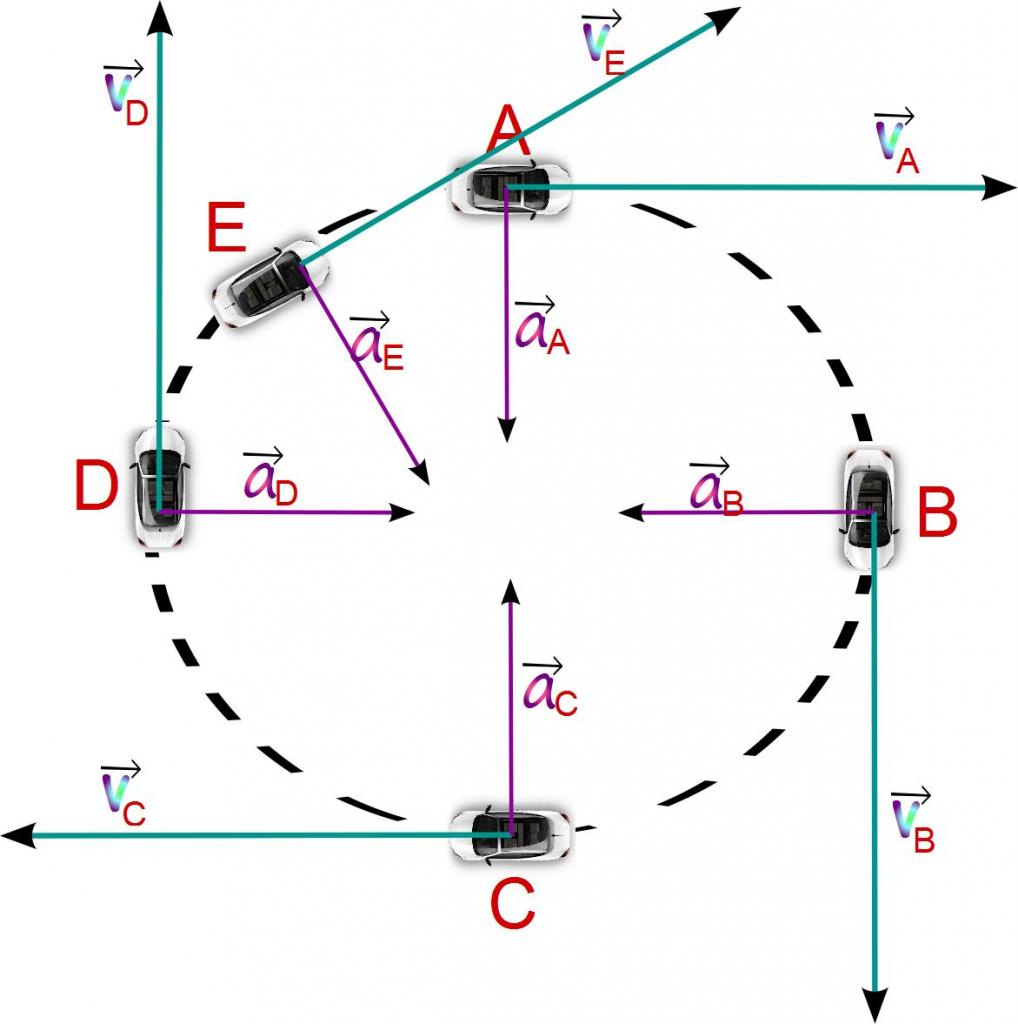
Biorąc pod uwagę takie przyspieszenie, konieczne jest rozważenie odpowiedniej charakterystyki kątowej.

Powyżej wprowadzono pojęcie prędkości kątowej, która jest mierzona w radianach na sekundę (rad / s). Jeśli znajdziemy pochodną tej prędkości względem czasu, wówczas uzyskamy wielkość przyspieszenia kątowego:

α¯ = ω¯ / dt

Łatwo jest pokazać, że wartość kątowa jest związana ze styczną składową pełnego przyspieszenia przez następującą zależność:

a _t = α × r

Przy stałym przyspieszeniu kątowym, składowa styczna a będzie większa dla punktów położonych dalej od osi obrotu.

Przyspieszenie kątowe nie ma nic wspólnego z normalnym komponentem.

Rozwiązywanie problemu określania przyspieszenia

Załóżmy, że poruszając się z przyspieszeniem stałym wzdłuż linii prostej, ciało pokonało dystans 100 metrów. Wiadomo, że początkowa prędkość ciała wynosiła 1 m / s. Ciało pokonało zaznaczoną odległość w 5,5 sekundy. Jakie jest przyspieszenie ruchu?

W zależności od stanu problemu mówimy o równomiernie przyspieszonym ruchu po prostej trajektorii. Przebyta ścieżka w tym przypadku może być obliczona za pomocą następującego wzoru:

L = v ₀ × t + a × t 2/2

Wyrażając z równości wartość a, mamy:

a = 2 × (L - v × × t) / t ²

Wszystkie wartości po prawej stronie równości są znane z tego warunku. Zastąp je i napisz odpowiedź: a = 6,25 m / s ² . Oznacza to, że podczas każdego z 5,5 sekund prędkość ciała wzrasta o 6,25 m / s. Znaleziona wartość całkowitego przyspieszenia pokrywa się z komponentem stycznym.