Jaka jest stała grawitacyjna?
Po przestudiowaniu przebiegu fizyki w umysłach studentów są wszelkiego rodzaju trwałe i ich wartości. Temat grawitacji i mechaniki nie jest wyjątkiem. Najczęściej nie potrafią odpowiedzieć na pytanie, jak ważna jest stała grawitacyjna. Ale zawsze jednoznacznie odpowiedzą, że jest ona obecna w prawie świata.
Z historii stałej grawitacyjnej
Co ciekawe, w twórczości Newtona nie ma takiej wielkości. Pojawiła się w fizyce dużo później. Dokładniej mówiąc, był to dopiero początek XIX wieku. Ale to nie znaczy, że tak nie było. Naukowcy po prostu nie rozpoznali go i nie rozpoznali jego dokładnego znaczenia. Mówiąc o znaczeniu. Grawitacyjny stałe stale jak określono dziesiętny z dużą liczbą cyfr po przecinku dziesiętnym, przed którym znajduje się zero.
Właśnie dlatego, że ta ilość przyjmuje tak małą wartość, że działanie sił grawitacji jest niedostrzegalne na małych ciałach. Właśnie z powodu tego mnożnika siła przyciągania okazuje się być nieistotna.
Po raz pierwszy eksperymentalnie ustalił wartość przyjętą przez stałą grawitacyjną, fizyka G. Cavendisha. I stało się to w 1788 roku.

W swoich eksperymentach używał cienkiego pręta. Został zawieszony na cienkim miedzianym druciku i miał długość około 2 metrów. Dwie identyczne ołowiane kulki o średnicy 5 cm zostały przymocowane do końców tego pręta, a obok umieszczono duże ołowiane kulki. Ich średnica wynosiła już 20 cm.
Przy zbliżaniu się dużych i małych kulek zaobserwowano rotację pręta. Mówiło o ich atrakcyjności. Ze znanych mas i odległości, a także ze zmierzonej siły skręcającej, można było dość dokładnie ustalić, jaka jest stała grawitacyjna.
Wszystko zaczęło się od swobodnego upadku ciał.
Jeśli umieścimy ciała o różnej masie w pustce, spadną one w tym samym czasie. Pod warunkiem, że spadną z tej samej wysokości i zaczną w tym samym czasie. Możliwe było obliczenie przyspieszenia, z jakim wszystkie ciała spadają na Ziemię. Okazało się, że jest w przybliżeniu równa 9,8 m / s 2 .
Naukowcy odkryli, że siła, z jaką wszystko jest przyciągane do Ziemi, jest zawsze obecna. I nie zależy od wysokości, na jaką się porusza. Jeden metr, kilometr lub setki kilometrów. Bez względu na to, jak daleko znajduje się ciało, przyciągnie ono Ziemię. Kolejne pytanie brzmi, jak jego wartość będzie zależeć od odległości?
Właśnie na to pytanie angielski fizyk I. Newton znalazł odpowiedź.
Zmniejszenie siły przyciągania ciał z ich odległości
Na początek zasugerował, że siła grawitacji maleje. A jego wartość jest odwrotnie proporcjonalna do odległości do kwadratu. Co więcej, odległość ta musi być liczona od środka planety. I wykonał teoretyczne obliczenia.
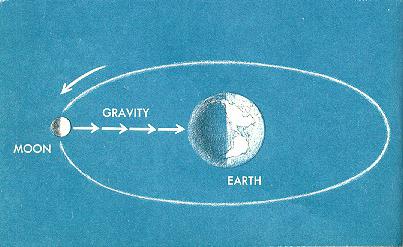
Następnie naukowiec wykorzystał dane astronomów dotyczące ruchu naturalnego satelity Ziemi - Księżyca. Newton obliczył przyspieszenie, z jakim obraca się wokół planety, i uzyskał takie same wyniki. To świadczyło o prawdziwości jego rozumowania i pozwalało je formułować prawo świata. Stała grawitacyjna w jego formule była dotychczas nieobecna. Na tym etapie ważne było określenie zależności. Co zostało zrobione. Grawitacja zmniejsza się odwrotnie do kwadratu kwadratu odległości od centrum planety.
Do prawa świata
Newton kontynuował myślenie. Ponieważ Ziemia przyciąga Księżyc, to samo powinno przyciągać Słońce. Co więcej, siła takiego przyciągania powinna również być zgodna z prawem przez niego opisanym. A potem Newton rozprzestrzenił go na wszystkie ciała wszechświata. Dlatego nazwa prawa zawiera słowo "uniwersalny".
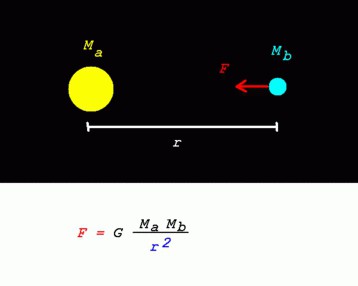
Siły ciał ogólnoświatowych określa się jako proporcjonalnie zależne od iloczynu mas i odwrotnie do kwadratu odległości. Później, kiedy ustalono współczynnik, formuła prawa uzyskała następującą formę:
- F t = G (m 1 * x m 2 ): r 2 .
Zawiera następujący zapis:
| Siła | F t |
| Stała grawitacyjna | G |
| Masa ciała | m 1 , m 2 |
| Odległość między ciałami | r |
Wzór tej stałej grawitacyjnej wynika z tego prawa:
- G = (F t X r 2 ): (m 1 x m 2 ).
Wartość stałej grawitacyjnej
Teraz przyszła kolej na konkretne liczby. Ponieważ naukowcy stale wyjaśniają tę wartość, różne liczby zostały oficjalnie przyjęte w różnych latach. Na przykład, zgodnie z danymi dla 2008 r., Stała grawitacyjna wynosi 6,6742 x 10 -11 Nˑm 2 / kg 2 . Minęły trzy lata - i stała się liczona. Teraz stała grawitacyjna wynosi 6,6738 x 10 -11 Nˑm 2 / kg 2 . Ale dla dzieci w wieku szkolnym w rozwiązywaniu problemów dopuszczalne jest zaokrąglenie do takiej wartości: 6,67 x 10 -11 Nˑm 2 / kg 2 .
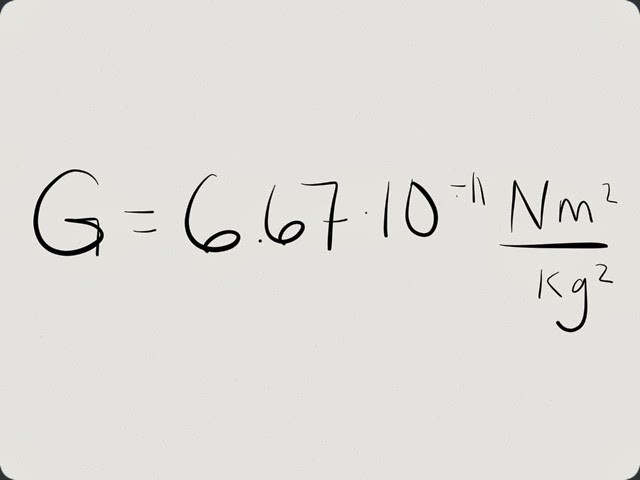
Jakie jest fizyczne znaczenie tego numeru?
Jeśli w formule, która jest podana dla prawa świata, aby zastąpić konkretne liczby, otrzymasz ciekawy rezultat. W szczególnym przypadku, gdy masy ciał są równe 1 kilogramowi i znajdują się w odległości 1 metra, siła siły jest równa samej liczbie, która znana jest dla stałej grawitacyjnej.
Oznacza to, że znaczenie stałej grawitacyjnej pokazuje, z jaką siłą przyciągają takie ciała w odległości jednego metra. Według liczby można zobaczyć, jak mała jest ta siła. W końcu jest to dziesięć miliardów mniej niż jeden. Nawet nie można tego zauważyć. Nawet ze wzrostem ciała sto razy wynik nie zmieni się znacząco. Wciąż pozostaje znacznie mniej niż jeden. Dlatego staje się jasne, dlaczego siła przyciągania jest zauważalna tylko w tych sytuacjach, gdy co najmniej jedno ciało ma ogromną masę. Na przykład planeta lub gwiazda.
Jak jest stała grawitacyjna z przyspieszeniem swobodny spadek?
Jeśli porównamy dwie formuły, z których jedna dotyczy grawitacji, a druga prawa ziemskiego, widzimy prosty wzór. Stała grawitacji, masa Ziemi i kwadrat odległości od środka planety stanowią współczynnik, który jest równy przyspieszyć swobodny spadek. Jeśli napiszesz tę formułę, otrzymasz następujące informacje:
- g = (G x M): r 2 .
I używa następującej notacji:
| Masa ziemi | M |
| Promień Ziemi | r |
Nawiasem mówiąc, z tej formuły można znaleźć stałą grawitacyjną:
- G = (g x r 2 ): M.
Jeśli chcesz poznać przyspieszenie swobodnego spadania na pewnej wysokości nad powierzchnią planety, ta formuła jest przydatna:
- g = (G x M): (r + n) 2 , gdzie n jest wysokością nad powierzchnią ziemi.
Zadania wymagające znajomości stałej grawitacyjnej
Pierwsze zadanie
Stan Jakie jest przyspieszenie swobodnego spadania na jedną z planet Układu Słonecznego, na przykład na Marsie? Wiadomo, że jego masa wynosi 6,23 · 10 23 kg, a promień planety wynosi 3,38 · 10 6 m.
Decyzja . Musisz użyć formuły, która została napisana dla Ziemi. Tylko do zastąpienia w nim wartości podanych w zadaniu. Okazuje się, że przyspieszenie swobodnego spadania będzie równe iloczynowi 6,67 x 10 -11 i 6,23 x 10 23 , które następnie należy podzielić na kwadrat o wartości 3,38 · 10 6 . W liczniku uzyskano wartość 41,55 x 10 12 . A mianownik wyniesie 11,42 x 10 12 . Stopnie zostaną zmniejszone, dlatego do odpowiedzi wystarczy znać tylko iloraz dwóch liczb.
Odpowiedź : 3,64 m / s 2 .
Zadanie Drugie
Stan Co należy zrobić z ciałami, aby zredukować siłę grawitacji o 100 razy?
Decyzja . Ponieważ masy ciał nie można zmienić, siła będzie się zmniejszać z powodu ich wzajemnego usuwania. Sto otrzymuje się z kwadratu 10. Oznacza to, że odległość między nimi powinna być 10 razy większa.
Odpowiedź : odległość je 10 razy od pierwotnej odległości.