Jak nazywa się czworobok pod kątem prostym?

Badanie geometrii rozpoczyna się od rozważenia prostych figur na płaszczyźnie łatwej do wyobrażenia przy użyciu abstrakcyjnej wyobraźni. Jedną z takich figur jest czworokąt z prostymi kątami. W III klasie szkół powszechnych zaczynają się z nią zapoznawać i szczegółowo badać jego właściwości w klasach wyższych. Weź pod uwagę główne cechy tej postaci w artykule, a także podaj przykłady jej wykorzystania w życiu codziennym.

Jak nazywa się czworokąt z prostymi kątami?

Słowo "czworobok" mówi, że figurka składa się z czterech rogów. W samolocie będzie zamknięty tylko wtedy, gdy ma cztery proste boki. Jeśli przeciwległe boki są parami równoległe do siebie, wówczas taką figurę nazywa się równoległobokiem. Jego cztery rogi są równe parami, ale mogą przyjmować dowolne wartości od 0 ^o do 180 ^o . Jeśli wszystkie jego kąty są równe 90 ^o , wówczas nazywa się je prostymi. Czworoboczny z prostymi kątami jest prostokącie, a jednocześnie jest równoległobokiem.

Prostokąt charakteryzuje się tylko dwoma parametrami: długościami sąsiednich boków. W dalszej części artykułu oznaczymy je jako a i b. Jeśli te długości są sobie równe, prostokąt ulega degeneracji do kwadratu.

Formuła kwadratowa

Prostokąt to idealna figura, na którą osoba podczas swojego życia próbuje dopasować otaczające przedmioty, na przykład cegłę, kształt dziedzińca przed domem, monitor komputerowy i tak dalej. Dlatego często występuje problem z obliczaniem obszaru prostokąta.

Oblicz obszar danej postaci nie jest trudny. Ponieważ prostokąt jest równoległobokiem, jego powierzchnię oblicza się jako iloczyn dwóch długości: wysokości, obniżonej po jednej stronie i po tej stronie. Wysokość równoległoboku jest znaleziona jako wynik sinusa jednego z jego narożników i boku. Ponieważ rozważamy konkretny rodzaj równoległoboku - prostokąta, to sinus pod kątem prostym jest równy jeden, co oznacza, że ​​poszukiwana formuła dla obszaru przyjmuje następującą postać:

S = a * b

Pole czworokąta o kącie prostym jest równe iloczynowi długości dwóch nierównoległych boków.

Poniżej zostanie pokazane, jak znaleźć obszar prostokąta, jeśli znane są jego inne elementy, na przykład długość przekątnej.

Prostokąt po przekątnej

Poniższy rysunek pokazuje dowolny czworobok z prostymi kątami i dwiema przekątnymi.

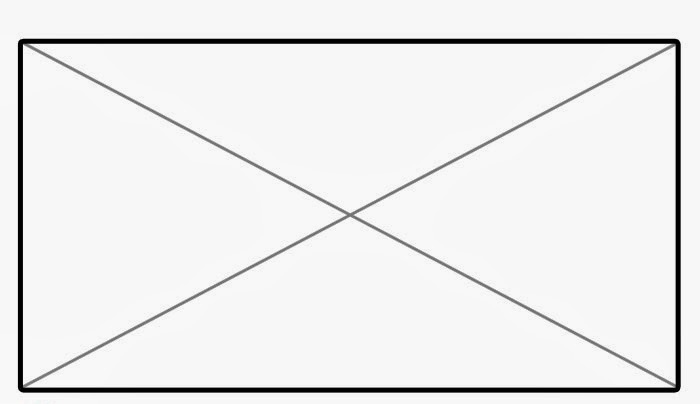
Widać, że przekątne dzielą się na dwie części, przeciwne kąty proste na figurze. Oznaczymy punkt przecięcia przekątnych przez symbol C. Jest to ważne, ponieważ jest to środek symetrii figury. Długości obu przekątnych są równe.

Przekątne dzielą prostokąt na cztery trójkąty równoramienne, dla których łatwo jest obliczyć długości boków i obszaru. Co dwa trójkąty, których podstawy leżą na bokach o równej długości prostokąta, są takie same.

Jeśli trzymasz jedną przekątną, podzieli prostokąt na dwa całkowicie identyczne trójkąty. Fakt ten pozwala na użycie twierdzenia Pitagorasa do obliczenia długości przekątnej, znając nogi trójkąta. Poniższy rysunek pokazuje, jak znaleźć kwadrat przekątnej c prostokąta. Tutaj przekątna jest przeciwprostokątna, a boki prostokąta odpowiadają nogom trójkąta.

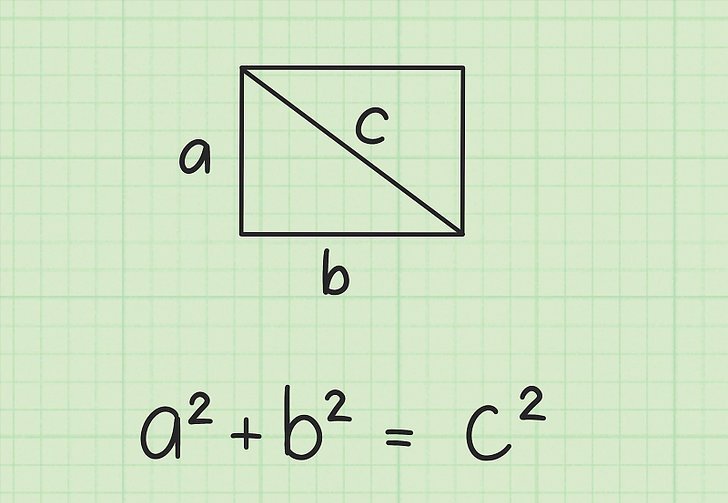
Wtedy wartość długości c będzie równa:

c = √ (a ² + b ² )

Prostokąt symetrii

Jak zauważono, środkiem symetrii jest punkt C utworzony przez przecinające się przekątne. Biorąc pod uwagę figurę na płaszczyźnie, możemy powiedzieć, że oś przechodząca przez ten punkt i równoległa do dwóch boków prostokąta jest osią symetrii drugiego rzędu, to znaczy obrót wokół o 180 ^o przełoży prostokąt na siebie. Ponieważ rozważany czworokąt ma dwie pary równoległych boków, oczywiste jest, że ma dwie określone osie symetrii.

Oś symetrii dzieli kształt na dwa identyczne prostokąty z bokami:

a i b / 2 lub b oraz a / 2

Niektóre właściwości geometryczne prostokąta

Ponieważ dana figura ma pewną symetrię, ma kąty proste i parami równoległymi, ponieważ możliwe jest zidentyfikowanie wielu ważnych właściwości używanych w praktyce. Wymieniamy je:

1. Każda linia przechodząca przez środek C figury przecina ją w dwóch punktach w tej samej odległości od punktu C. Maksymalna odległość od C do boku przekątnej prostokąta jest równa połowie długości przekątnej, minimalna odległość jest równa połowie długości jego krótszego boku.
2. Jeśli podzielimy jedną stronę prostokąta na pół, to łącząc ten punkt z wierzchołkami przeciwległej strony równoległej, otrzymamy trójkąt równoramienny o powierzchni równej połowie powierzchni prostokąta.
3. Jeśli opisany powyżej punkt zostanie przesunięty ze środka boku na jeden lub drugi koniec, wówczas równania zaznaczonego trójkąta zostaną naruszone, ale jego obszar pozostanie niezmieniony.
4. Każdy prostokąt można wprowadzić w kółko.

Pierwsza właściwość jest oczywista, ponieważ każda prosta przechodząca przez C będzie przecinać równoległe boki kształtu. Dowieramy pozostałe właściwości.

Dowód właściwości 2, 3 i 4

Najpierw rozważmy właściwości 2 i 3. Poniższy rysunek pokazuje prostokąt z trzema trójkątami na bokach:

ABC ₁ , ABC ₂ i ABC ₃

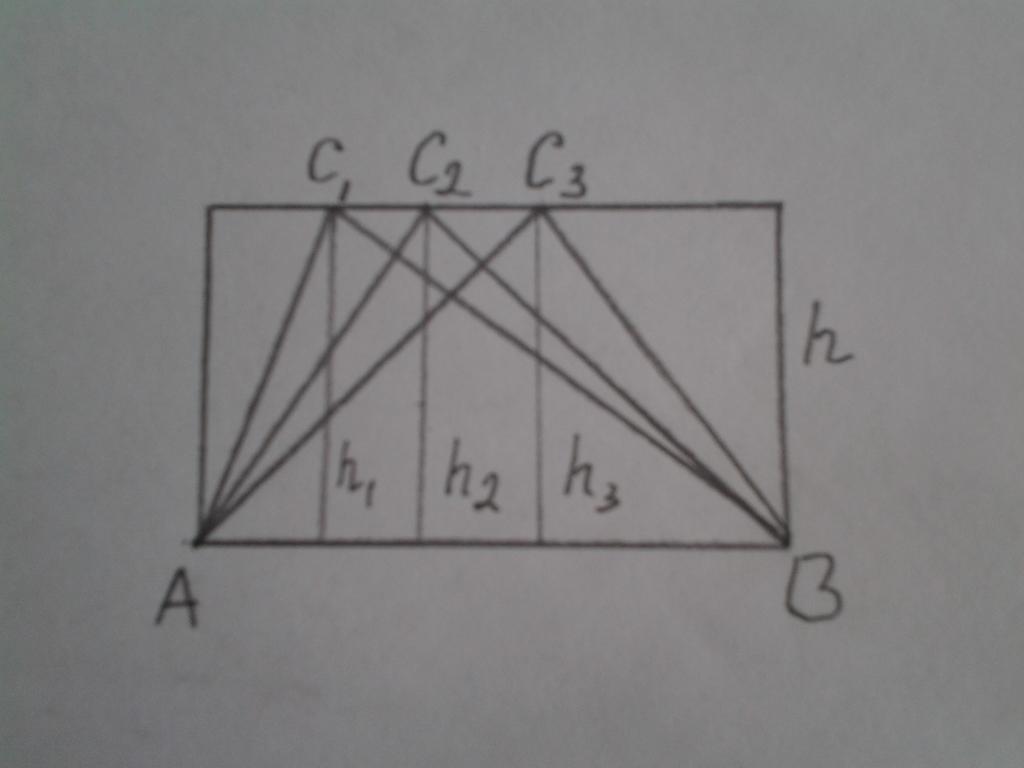
Zgodnie ze wzorem na znalezienie obszaru trójkąta, można je zapisać:

S ₁ = 1/2 * h ₁ * AB;

S ₂ = 1/2 * h ₂ * AB;

S ₃ = 1/2 * h ₃ * AB

Można zauważyć, że wszystkie wysokości h _i rozpatrywanych trójkątów są równe długości boku h prostokąta. Oznacza to, że ich obszary są równe:

S ₁ = S ₂ = S ₃

Teraz piszemy wzór dla obszaru S prostokąta i dzielimy S przez obszar jednego z przedstawionych trójkątów, otrzymujemy:

S = AB * h;

S / S ₁ = AB * h / (1/2 * h * AB) = 2

Tak więc prostokąt ma obszar dwukrotnie większy niż którykolwiek z przedstawionych trójkątów, czyli udowodniliśmy drugą i trzecią właściwość.

Jeśli chodzi o możliwość wpisania czworokąta pod kątem prostym w kole, należy tutaj argumentować w następujący sposób: narysujemy przekątne rysunku, przecinają się one w punkcie C. Ponieważ punkt ten znajduje się w tej samej odległości od czterech wierzchołków prostokąta, może służyć jako środek okręgu. Jeśli promień okręgu jest równy połowie długości przekątnej, to linia koła przejdzie przez wszystkie cztery wierzchołki prostokąta, to znaczy, że zostanie w nim wpisana.

Czy czworokąt z pojedynczym kątem to linia, prostokąt?

Odpowiedź na pytanie będzie pozytywna tylko w przypadku, gdy czworobok jest równoległobokiem. W takim przypadku, jeśli jeden kąt jest równy 90 ^o , wówczas dwa pozostałe sąsiednie kąty będą również proste, co oznacza, że ​​czwarty kąt będzie równy 90 ^o . Znaleźliśmy właściwe kąty w czworokącie wszystko, co oznacza, że ​​jest to prostokąt.

Jeśli czworobok o jednym kącie prostym nie ma par równoległych, to nie będzie to prostokąt.

Gdzie jest używany prostokąt i jego właściwości?

Przy wytwarzaniu arkuszy tetradowych należy stosować kształt prostokątny, a stosunek długości większego boku do mniejszego wynosi √2. Ten kształt figury prowadzi do tego, że jeśli jest ona podzielona na pół przez symetryczną oś równoległą do większego boku, wówczas utworzone dwa nowe prostokąty będą miały współczynnik kształtu √2. Taki podział może być kontynuowany do nieskończoności, podczas gdy kształt otrzymanych prostokątów zostanie zachowany.

Prostokątny kształt służy do produkcji ekranów telewizyjnych. Przed erą monitorów ciekłokrystalicznych (LCD) używano ekranów z wiązką elektronów, których współczynnik kształtu wynosił 4: 3. Wraz z pojawieniem się monitorów LCD o wysokiej rozdzielczości, zaczęli stosować nowy standard: 16: 9.

Mozaika, która zdobi ściany budynków, ma kształt czworoboku z prostymi kątami.

Obliczanie powierzchni figury wzdłuż znanej przekątnej

Kończymy artykuł, rozważając kwestię obliczania obszaru czworoboku, którego wierzchołki kątów prostych są połączone przekątną. Oblicz obszar nowoczesnego monitora LCD, jeśli wiadomo, że jego przekątna wynosi c = 35 cm.

Ten problem można rozwiązać, ponieważ monitor ma standardowy format obrazu 16: 9. Oznaczając x jako nieznany współczynnik, otrzymujemy długości boków monitora:

a = 16 * x;

b = 9 * x

Teraz stosujemy formułę do określenia przekątnej, otrzymujemy:

c ² = a ² + b ² =>

35 ² = x ² * (16 ² +9 ² ) =>

x = 35 / √ (16 ² +9 ² ) ≈ 1,9

Następnie boki monitora i jego powierzchnia są równe:

a = 16 * x = 30,4 cm;

b = 9 x = 17,1 cm;

S = a * b ≈ 520 cm ²

Po raz kolejny zauważamy, że obszar może być określony przez wartość przekątnej tylko wtedy, gdy znany jest stosunek boków prostokąta.