Diagonal cube: co to jest i jak go znaleźć?
Przekątna sześcianu jest jednym z elementów, które trzeba znać przy rozwiązywaniu problemów w stereometrii podczas ukończenia końcowego zadania z matematyki na potrzeby szkoły podstawowej.
Teoria kostki
Ten wielościan odnosi się bezpośrednio do prostych równoległościanów i pryzmatów. Jest szczególnym przypadkiem obu. U podstawy sześcianu leży kwadrat, a jego boczne krawędzie są równe stronie danego kwadratu. A więc wszystko trzy wymiary mają te same wartości.
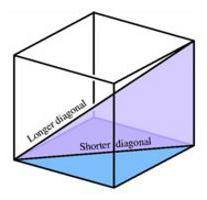
Wszystkie sześć ścian sześcianu to kwadraty. Długość każdej z 12 krawędzi jest taka sama.
W każdej z powierzchni można narysować przekątną, której długość można łatwo znaleźć za pomocą formuły pitagorejskiej. Ponadto sam sześcian ma przekątną. Jest ich tylko czterech. Przekątna sześcianu jest narysowana w taki sposób, aby rozpoczynała się od góry dolnej podstawy. Koniec tego segmentu znajduje się u góry górnej podstawy, ale tak, aby nie pokrywał się z przekątną kwadratu.
Ad
Ważne formuły
Będą musieli wpisać to samo oznaczenie. Najczęściej litera "a" jest bokiem sześcianu. "V" ma objętość. "S" i "d" oznaczają odpowiednio powierzchnię i przekątną. "R" i "r" promienie opisywanych i wpisanych sfer.
V = a³ (# 1) służy do znalezienia objętości;
S = a² (# 2) wzór dla powierzchni twarzy;
S = 6a² ( №3 ) jest konieczne do obliczenia powierzchni całej powierzchni sześcianu;
jeśli chcesz poznać przekątną sześcianu, formuła będzie taka d = a √ 3 (# 4);
przydatne do wyszukiwania promieni: R = (a / 2) * √3 i r = a / 2 (nr 5) i (nr 6) .
Kilka słów o symetrii sześcianu
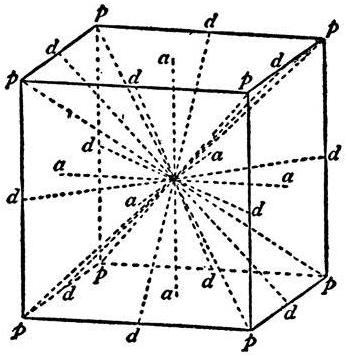
Ten geometryczny obiekt ma dwa typy symetrii: względem punktu i osi. Aby znaleźć pierwszą, musisz narysować przekątną sześcianu, a następnie drugą, aby znaleźć punkt przecięcia. Będzie centrum symetrii.
Ad
Wszystkie linie, które przechodzą przez ten punkt i są prostopadłe do powierzchni, są osiami symetrii.
Przykłady zadań z egzaminu
Są one używane w części B, to znaczy tam, gdzie trzeba wykonać szczegółowe rozwiązanie zadania. Po prostu wybierz odpowiedź, która się nie powiedzie. Dlatego konieczne jest poznanie formuł i umiejętność ich zastosowania w różnych sytuacjach.
Pierwsza grupa zadań. Zna długość przekątnej sześcianu. Wymagane jest obliczenie jego objętości lub określenie powierzchni.
Na przykład znana wartość może być równa jednej. Następnie, aby dowiedzieć się objętość i obszar, należy użyć wzorów nr 1 i 3. Ale mówią o krawędzi i ze względu na przekątną. Musisz napisać inną formułę.
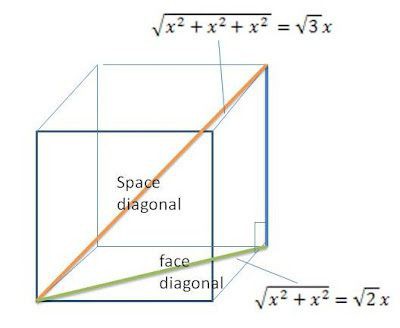
Jeśli spojrzysz na rysunek sześcianu i narysowaną na nim przekątną, zobaczysz, jakie formy trójkąt prostokątny. Jedna z jego nóg pokrywa się z krawędzią, druga z przekątną twarzy, a przekątna sześcianu jest przeciwprostokątną.
Następnie możemy napisać twierdzenie Pitagorasa: kwadrat przeciwprostokątnej (d 2 ) jest równy kwadratowi pierwszej nogi (a 2 ), złożonej z kwadratem drugiego (a√2) 2 . Po wykonaniu transformacji okazuje się, że krawędź sześcianu jest tak połączona z przekątną, która jest równa d podzielona przez pierwiastek kwadratowy z 3.
Teraz możesz zacząć znajdować krawędź, a następnie obliczyć objętość i powierzchnię. W konkretnym problemie, a = 1 / √3 = (√3) / 3. Następnie głośność jest równa (√3) / 9. Obszar jest dwa.
Druga grupa zadań. Odwrotna poprzednia, gdy znany jest obszar lub objętość, i wymagane jest obliczenie wartości przekątnej sześcianu.
Przykładem jest problem, w którym powierzchnia jest znana i jest równa 8. Konieczne będzie użycie wzoru nr 3 i zależności, która została uzyskana w poprzednim problemie.
Najpierw musisz znać długość krawędzi. Ona jest równa pierwiastek kwadratowy od częściowego S do 6. Po podstawieniu znanej ilości, a = √ (8/6) = √ (4/3). Teraz pozostaje obliczyć przekątną sześcianu, podnosząc tę liczbę i mnożąc ją przez 3. Okazuje się, że 2.
Trzecia grupa zadań zawiera dane o przekątnej powierzchni sześcianu. Muszą rozpoznać objętość lub powierzchnię ciała. Jest również możliwa opcja, w której należy obliczyć przekątną sześcianu. W takich problemach rozumowanie podąża tą samą ścieżką, którą rozważano w poprzednich przypadkach.