Punkt materialny: definicja, wartości, przykłady i rozwiązywanie problemów

Jaki jest punkt materialny? Jakie wielkości fizyczne są z nią powiązane, dla których generalnie wprowadzono pojęcie punktu materialnego? W tym artykule omówimy te kwestie, podamy przykłady problemów związanych z omawianą koncepcją, a także omówimy formuły stosowane do ich rozwiązania.

Definicja

Więc jaki jest sens materialny? Różne źródła podają definicję w nieco innym stylu literackim. To samo dotyczy nauczycieli na uniwersytetach, w kolegiach i instytucjach edukacyjnych. Jednak zgodnie z normą punkt materialny nazywany jest ciałem, którego wymiary (w porównaniu z wymiarami ramy odniesienia) można pominąć.

Połączenie z prawdziwymi obiektami

Wydawałoby się, jak można wziąć osobę, rowerzystę, samochód, statek, a nawet samolot, jako punkt materialny, z którymi w przypadku mechaniki poruszającego się ciała radzą sobie głównie problemy fizyczne? Spójrzmy głębiej! Aby określić współrzędne poruszającego się ciała w dowolnym momencie, konieczne jest poznanie kilku parametrów. Jest to początkowa współrzędna, szybkość ruchu i przyspieszenie (jeśli to oczywiście nastąpi) i czas.

Co jest potrzebne, aby rozwiązać problemy z punktami materialnymi?

Relacje współrzędnych można znaleźć tylko poprzez dołączenie do układu współrzędnych. Nasza planeta staje się takim rodzajem układu współrzędnych dla samochodu i innego ciała. I w porównaniu z jego wielkością, rozmiar ciała może być naprawdę zaniedbany. Odpowiednio, jeśli przyjmujemy ciało jako punkt materialny, jego współrzędną dwuwymiarową (trójwymiarowa) przestrzeń może i powinien być znaleziony jako współrzędna punktu geometrycznego.

Ruch punktu materialnego. Zadania

W zależności od złożoności zadania mogą uzyskać określone warunki. Odpowiednio, w oparciu o podane warunki, możemy użyć pewnych formuł. Czasami, nawet z całym arsenałem formuł, nadal nie jest możliwe rozwiązanie problemu, jak mówią, "head on". Dlatego niezwykle ważne jest nie tylko poznanie kinematycznych wzorów związanych z punktem materialnym, ale także umiejętność ich wykorzystania. To znaczy, aby wyrazić pożądaną wartość i zrównać układ równań. Oto podstawowe formuły, które zastosujemy w trakcie rozwiązywania problemów:

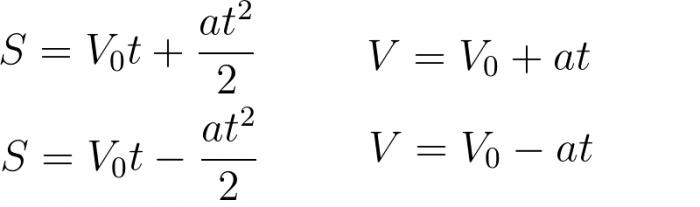
Numer problemu 1

Samochód, stojąc na linii startu, nagle zaczyna poruszać się z pozycji stacjonarnej. Dowiedz się, która godzina przyspieszy do 20 metrów na sekundę, jeśli jego przyspieszenie wynosi 2 metry na sekundę do kwadratu.

Po prostu chcę powiedzieć, że to zadanie jest praktycznie najprostszą rzeczą, jakiej uczeń może się spodziewać. Słowo "praktycznie" stoi tutaj z jakiegoś powodu. Chodzi o to, że łatwiej jest zastąpić bezpośrednie wartości w formułach. Najpierw powinniśmy wyrazić czas, a następnie dokonać obliczeń. Aby rozwiązać problem, potrzebujemy wzoru do wyznaczenia chwilowej prędkości (chwilowa prędkość jest prędkością ciała w określonym punkcie czasu). Ma następującą postać:

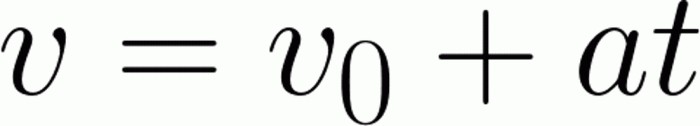
Jak widać po lewej stronie równania mamy chwilową prędkość. Absolutnie go tam nie potrzebujemy. Dlatego wykonujemy proste operacje matematyczne: pozostawić produkt przyspieszenia przez chwilę po prawej stronie i przenieść początkową prędkość w lewo. W tym samym czasie należy uważnie śledzić znaki, ponieważ jeden niepoprawnie pozostawiony znak może radykalnie zmienić odpowiedź na zadanie. Następnie nieco komplikujemy wyrażenie, pozbywając się przyspieszenia po prawej stronie: dziel się przez to. W rezultacie, po prawej stronie, powinniśmy mieć czysty czas, po lewej, dwupoziomowy wyraz. Cała sprawa jest po prostu zamieniona, żeby wyglądać znajomo. Pozostaje tylko zastąpić wartości. Okazuje się, że samochód przyspieszy w 10 sekund. Ważne: rozwiązaliśmy problem, zakładając, że punkt materialny znajduje się w samochodzie.

Numer problemu 2

Punkt materialny rozpoczyna hamowanie awaryjne. Ustal, jaka była początkowa prędkość podczas hamowania awaryjnego, jeżeli minęło 15 sekund, zanim nastąpiło całkowite zatrzymanie nadwozia. Przyspieszenie wynosi 2 metry na sekundę do kwadratu.

Zadanie jest z zasady bardzo podobne do poprzedniego. Ale jest kilka ich niuansów. Najpierw musimy określić prędkość, którą zwykle nazywamy prędkością początkową. Oznacza to, że w pewnym momencie rozpoczyna się odliczanie czasu i odległości przebytej przez ciało. Szybkość w tym przypadku rzeczywiście będzie wchodzić w zakres tej definicji. Drugi niuans jest oznaką przyspieszenia. Przypomnij sobie, że przyspieszenie jest wielkością wektora. W konsekwencji, w zależności od kierunku, zmieni swój znak. Przyspieszenie dodatnie obserwuje się, gdy kierunek prędkości ciała pokrywa się z kierunkiem. Po prostu, kiedy ciało przyspiesza. W przeciwnym razie (czyli w naszej sytuacji hamowania) przyspieszenie będzie ujemne. Te dwa czynniki należy rozważyć, aby rozwiązać ten problem:

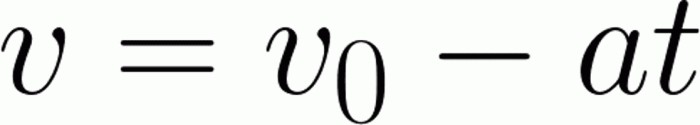
Podobnie jak ostatnim razem, najpierw wyrażamy potrzebną wartość. Aby uniknąć bałaganu ze znakami, zostawiamy początkową prędkość tam, gdzie jest. Z przeciwnym znakiem przenosimy na drugą część równania iloczyn przyspieszania w czasie. Od momentu zakończenia hamowania prędkość końcowa wynosi 0 metrów na sekundę. Zastępując te i inne wartości, łatwo znajdujemy początkową prędkość. Będzie równa 30 metrów na sekundę. Łatwo zauważyć, że znając formuły, nie jest tak trudno poradzić sobie z najprostszymi zadaniami.

Numer problemu 3

W pewnym momencie dyspozytorzy rozpoczynają śledzenie ruchu obiektu powietrznego. Jego prędkość w tym momencie wynosi 180 kilometrów na godzinę. Po czasie równym 10 sekund jego prędkość wzrasta do 360 kilometrów na godzinę. Określić odległość przebytą przez samolot podczas lotu, jeżeli czas lotu wynosił 2 godziny.

W rzeczywistości, w szerokim tego słowa znaczeniu, zadanie to ma wiele odcieni. Na przykład przyspieszenie samolotu. Oczywiste jest, że nasze ciało nie może poruszać się w zasadzie po prostej trajektorii. Oznacza to, że musi wystartować, podnieść prędkość, a następnie, na pewnej wysokości, jakiś odcinek odległości powinien poruszać się w linii prostej. Odchylenia nie są brane pod uwagę, a także spowolnienie samolotu podczas lądowania. Ale to nie jest nasza sprawa w tym przypadku. Dlatego rozwiążemy problem w ramach wiedzy szkolnej, ogólnej informacji o ruchu kinematycznym. Aby rozwiązać problem, potrzebujemy następującej formuły:

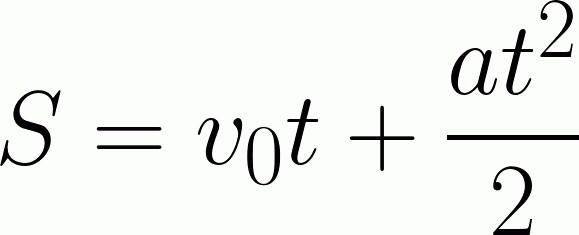
Ale tutaj czeka nas szkopuł, o którym mówiliśmy wcześniej. Znajomość formuł nie jest wystarczająca - trzeba umieć z nich korzystać. Oznacza to, że wyprowadź jedną wartość za pomocą alternatywnych formuł, znajdź ją i zastąp. Przeglądając początkowe informacje dostępne w zadaniu, natychmiast staje się jasne, że rozwiązanie problemu po prostu nie zadziała. Nic nie mówi się o przyspieszeniu, ale istnieją informacje o tym, jak prędkość zmieniła się w pewnym okresie czasu. Możemy więc samemu znaleźć przyspieszenie. Weź wzór na znalezienie chwilowej prędkości. Ona ma spojrzenie

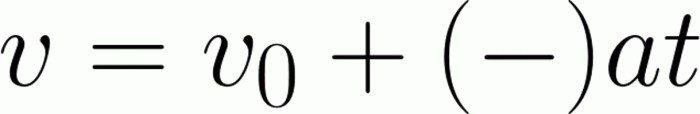
Przyspieszenie i czas pozostały w jednej części, a początkowa prędkość jest przenoszona na drugą. Następnie, dzieląc obie części na chwilę, zwalniamy prawą stronę. Tutaj możesz natychmiast obliczyć przyspieszenie, zastępując dane bezpośrednie. Ale znacznie lepiej jest wyrazić dalej. Wzór otrzymany dla przyspieszenia jest podstawiony do głównego. Tam możesz nieco zredukować zmienne: w liczniku czas jest podany w kwadracie, aw mianowniku - w pierwszym stopniu. Dlatego z tego mianownika można się pozbyć. No cóż - prosta podstawienie, ponieważ nie ma nic więcej do wyrażenia. Odpowiedź powinna brzmieć: 440 kilometrów. Odpowiedź będzie inna, jeśli przetłumaczysz wartości na inny wymiar.

Wniosek

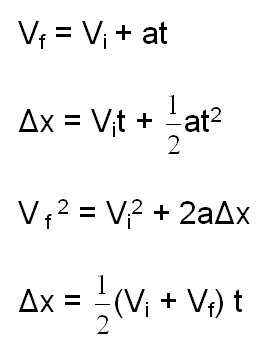
Co dowiedzieliśmy się w trakcie tego artykułu?

1) Punkt materialny jest ciałem, którego wymiary można pominąć w porównaniu do rozmiaru układu odniesienia.

2) Aby rozwiązać problemy związane z punktem materialnym, istnieje kilka formuł (podanych w artykule).

3) Znak przyspieszenia w tych formułach zależy od parametru ruchu ciała (przyspieszenie lub zwalnianie).