Obszar trapezowy: formuły i metody obliczeniowe

Aby czuć się pewnie i skutecznie rozwiązywać problemy na lekcjach geometrii, nie wystarczy uczyć się formuł. Muszą najpierw zrozumieć. Bać się, a jeszcze bardziej nienawidzić formuł, jest bezproduktywne. W tym artykule dostępny język przeanalizuje różne sposoby znalezienia obszaru trapezu. Aby lepiej opanować odpowiednie reguły i twierdzenia, zwrócimy uwagę na jego właściwości. Pomoże to zrozumieć, jak działają zasady i w jakich przypadkach te lub te formuły powinny być stosowane.

Określić trapezoid

Jaka jest ogólnie ta liczba? Trapezoid to wielokąt z czterech rogów o dwóch równoległych bokach. Pozostałe dwa boki trapezu można przechylać pod różnymi kątami. Jego równoległe boki są nazywane podstawami, a dla stron nierównoległych jest używana nazwa "boki" lub "biodra". Takie liczby są dość powszechne w życiu codziennym. Kontury trapezu można dostrzec w sylwetkach ubrań, elementach wyposażenia wnętrz, meblach, naczyniach i wielu innych. Trapezoid może być różnego rodzaju: uniwersalny, równoboczny i prostokątny. Więcej szczegółów na temat ich rodzajów i właściwości zostanie omówionych w dalszej części artykułu.

Właściwości trapezu

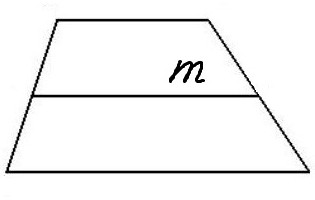Pokrótce omówmy właściwości tej figury. Suma kątów przylegających do każdej strony wynosi zawsze 180 °. Należy zauważyć, że wszystkie kąty trapezu dają do 360 °. Trapez ma koncepcję środkowej linii. Jeśli połączysz punkty środkowe boków z segmentem, będzie to środkowa linia. Jest to oznaczone jako m. Linia środkowa ma ważne właściwości: jest zawsze równoległa do podstaw (pamiętamy, że podstawy są również równoległe do siebie) i równa ich połowie:

m = (a + b) / 2.

Tej definicji należy się nauczyć i zrozumieć, ponieważ jest kluczem do rozwiązania wielu problemów!

W trapezie zawsze możesz obniżyć wysokość do podstawy. Wysokość jest prostopadła, często oznaczona symbolem h, która jest pobierana z dowolnego punktu jednej podstawy do drugiej bazy lub jej kontynuacji. Środkowa linia i wysokość pomogą znaleźć obszar trapezu. Takie zadania są najczęstsze w szkolnym kursie geometrii i regularnie pojawiają się w testach i egzaminach.

Najprostsze formuły obszaru trapezu

Przeanalizujmy dwie najpopularniejsze i najprostsze formuły, dzięki którym pomożemy znaleźć obszar trapezu. Wystarczy pomnożyć wysokość przez połowę sum zasad, aby łatwo znaleźć pożądane:

S = h * (a + b) / 2.

W tym wzorze a, b oznacza podstawę trapezu, h - wysokość. Dla wygody percepcji, w tym artykule znaki mnożenia są oznaczone symbolem (*) we wzorach, chociaż w oficjalnych książkach odniesienia znak pomnożenia jest zwykle pomijany.

Rozważ przykład.

Biorąc pod uwagę: trapez z dwiema podstawami równymi 10 i 14 cm, wysokość 7 cm Jaki jest obszar trapezu?

Przeanalizujmy rozwiązanie tego problemu. Zgodnie z tą formułą, najpierw musisz znaleźć pół sumy zasad: (10 + 14) / 2 = 12. Tak więc, połowa sumy wynosi 12 cm Teraz mnożymy połowę sumy przez wysokość: 12 * 7 = 84. Wymagane jest znalezione. Odpowiedź: powierzchnia trapezu wynosi 84 metry kwadratowe. patrz

Druga znana formuła mówi: powierzchnia trapezu jest równa iloczynowi linii środkowej i wysokości trapezu. W rzeczywistości wynika to z poprzedniej koncepcji środkowej linii: S = m * h.

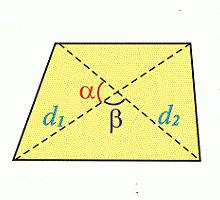
Używanie przekątnych do obliczeń

Inny sposób odnalezienia obszaru trapezowego nie jest w rzeczywistości tak skomplikowany. Jest to związane z jego przekątnymi. Zgodnie z tym wzorem, aby znaleźć obszar, konieczne jest pomnożenie półproduktu jego przekątnych (d ₁ d ₂ ) przez sinus kąta między nimi:

S = ½ d ₁ d ₂ sin a.

Rozważ zadanie, które pokazuje zastosowanie tej metody. Podano: trapez o długości przekątnych odpowiednio 8 i 13 cm, kąt a między przekątnymi wynosi 30 °. Znajdź obszar trapezu.

Decyzja. Korzystając z powyższego wzoru, łatwo jest obliczyć wymagane. Jak wiecie, grzech 30 ° wynosi 0,5. Dlatego S = 8 * 13 * 0,5 = 52. Odpowiedź: obszar ma 52 metry kwadratowe. patrz

Szukamy obszaru trapezu równobocznego.

Trapezoid może być równoboczny (równoramienny). Jego boki są takie same, a rogi w podstawie są równe, co dobrze ilustruje rysunek. Równoboczny trapez ma takie same właściwości jak zwykły i wiele specjalnych. Koło można opisać wokół trapezu uzbrojonego i można w nim wpisać okrąg.

Jakie są metody obliczania powierzchni takiej liczby? Następująca metoda będzie wymagać dużych obliczeń. Aby go użyć, musisz znać wartości sinusoidalne (sin) i cosinus (cos) kąta u podstawy trapezu. Aby je obliczyć, potrzebne są tabele Bradisa lub kalkulator inżynierski. Oto ta formuła:

S = c * sin a * ( a - c * cos a ),

gdzie c jest bocznym uchem, a jest kątem na dolnej podstawie.

Równoboczny trapez ma przekątne o tej samej długości. Odwrotność jest również prawdą: jeśli przekątna trapez jest równa, to jest to równoramienny. Stąd następująca formuła, która pomaga znaleźć obszar trapezu, jest półproduktem kwadratu przekątnych przy sinusoidzie kąta między nimi: S = ½ d ² sin a.

Znajdź obszar prostokątnego trapezu

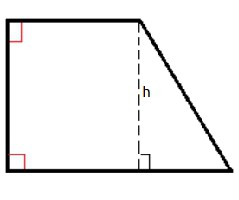
Znany specjalny przypadek prostokątny trapez. Jest to trapez, w którym jedna strona (jego udo) sąsiaduje z podstawami pod kątem prostym. Ma właściwości zwykłego trapezu. Ponadto ma bardzo interesującą funkcję. Różnica kwadratów przekątnych takiego trapezu jest równa różnicy kwadratów jego podstaw. W tym celu wykorzystują wszystkie wcześniej opisane metody obliczania powierzchni.

Zastosuj pomysłowość

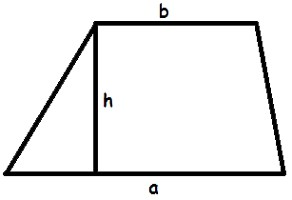
Jest jedna sztuczka, która może pomóc w przypadku zapomnienia określonych formuł. Zastanów się uważnie, co trapez. Jeśli podzielimy go mentalnie na części, poznamy i zrozumiemy geometryczne kształty: kwadrat lub prostokąt i trójkąt (jeden lub dwa). Jeśli wysokość i boki trapezu są znane, możesz użyć formuł obszar trójkąta i prostokąt, a następnie dodać wszystkie uzyskane wartości.

Ilustrujemy to za pomocą następującego przykładu. Mając prostokątny trapez. Kąt C = 45 °, kąty A, D to 90 °. Górna podstawa trapezu ma 20 cm, wysokość 16 cm, wymagane jest obliczenie powierzchni figury.

Rozwiązanie

Ta liczba oczywiście składa się z prostokąta (jeśli dwa kąty to 90 °) i trójkąta. Ponieważ trapez jest prostokątny, zatem jego wysokość jest równa bokowi, czyli 16 cm, mamy prostokąt o bokach odpowiednio 20 i 16 cm. Rozważmy teraz trójkąt, którego kąt wynosi 45 °. Wiemy, że jedna strona ma 16 cm, ponieważ ta strona jest jednocześnie wysokością trapezu (i wiemy, że wysokość spada do podstawy pod kątem prostym), dlatego drugi kąt trójkąta wynosi 90 °. W związku z tym pozostały kąt trójkąta wynosi 45 °. Konsekwencją tego jest otrzymanie prostokątnego trójkąta równoramiennego, którego dwa boki są takie same. Oznacza to, że druga strona trójkąta jest równa wysokości, to znaczy 16 cm Pozostaje obliczyć obszar trójkąta i prostokąta i dodać uzyskane wartości.

Obszar trójkąt prostokątny równy połowie iloczynu jego nóżek: S = (16 * 16) / 2 = 128. Obszar prostokąta jest równy iloczynowi jego szerokości przez długość: S = 20 * 16 = 320. Znaleźliśmy wymagany: obszar trapezu S = 128 + 320 = 448 kwadrat. patrz. Możesz łatwo sprawdzić siebie za pomocą powyższych formuł, odpowiedź będzie identyczna.

Użyj formuły Wybierz

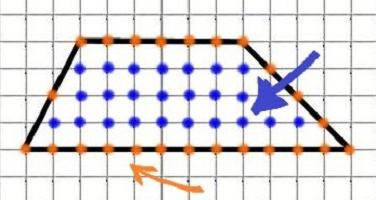
Na koniec przedstawiamy kolejną oryginalną formułę, która pomaga znaleźć obszar trapezu. Nazywa się to formułą Pick. Jest wygodny w użyciu, gdy trapez jest narysowany na papierze w kratkę. Podobne zadania często można znaleźć w materiałach GIA. Wygląda to tak:

S = M / 2 + N-1,

w tym wzorze M jest liczbą węzłów, tj. przecięcie linii figury z liniami komórki na granicach trapezu (pomarańczowe kropki na rysunku), N to liczba węzłów wewnątrz figury (niebieskie kropki). Najwygodniej jest go używać, gdy znajdujemy obszar nieregularnego wielokąta. Jednak im większy jest arsenał stosowanych metod, tym mniej błędów i lepszych wyników.

Oczywiście, dane informacje nie są wyczerpane przez rodzaje i właściwości trapezu, a także metody poszukiwania jego obszaru. Ten artykuł zawiera przegląd najważniejszych cech. W rozwiązywaniu problemów geometrycznych ważne jest, aby postępować stopniowo, zaczynać od prostych formuł i zadań, konsekwentnie utrwalać zrozumienie, przechodzić na inny poziom złożoności.

Zestawienie najpopularniejszych formuł pomoże uczniom zorientować się na różne sposoby obliczania powierzchni trapezu i lepiej przygotować się do testów i testów na ten temat.