Jakie trudności czekają na tych, którzy podjęli się dodania korzeni?
Temat pierwiastków kwadratowych jest obowiązkowy w szkolnym programie nauczania matematyki. Bez nich nie należy podejmować decyzji równania kwadratowe. A później staje się konieczne nie tylko wydobycie korzeni, ale także wykonywanie z nimi innych czynności. Wśród nich są dość złożone: potęgowanie mnożenie i dzielenie. Ale są dość proste: odejmowanie i dodawanie korzeni. Nawiasem mówiąc, na pierwszy rzut oka wydają się takie. Uruchamianie ich bez błędów nie zawsze jest łatwe dla kogoś, kto dopiero zaczyna się z nimi zapoznać.
Co to jest root matematyki?
Ta akcja powstała w opozycji do potęgowania. Matematyka zakłada istnienie dwóch przeciwstawnych operacji. Istnieje odejmowanie w celu dodania. Mnożenie jest przeciwstawiane przez dzielenie. Odwrotnością stopnia jest ekstrakcja odpowiedniego korzenia.
Ad

Jeśli w mocy są dwa, to korzeń będzie kwadratowy. Jest to najczęściej w matematyce szkolnej. Nie ma nawet wskazania, że jest kwadratowy, to znaczy, że nie przypisano mu liczby 2. Notacja matematyczna dla tego operatora (radykalna) jest pokazana na rysunku.
Z opisanej akcji płynnie podąża za swoją definicją. Aby wyodrębnić pierwiastek kwadratowy od pewnej liczby, musisz dowiedzieć się, który z nich da, gdy pomnoży się w tobie, radykalną ekspresję. Ta liczba będzie pierwiastkiem kwadratowym. Jeśli napiszesz to matematycznie, otrzymasz: x * x = x 2 = y, następnie √у = x.
Co możesz z nimi zrobić?
Rdzeń jest rdzeniem ułamkowym, w którym znajduje się jednostka w liczniku. A mianownikiem może być dowolny. Na przykład na pierwiastku kwadratowym jest równa dwa. Dlatego wszystkie działania, które można wykonać za pomocą stopni, będą ważne dla korzeni.
Ad
Wymagania dla tych działań są takie same. Jeśli mnożenie, dzielenie i potęgowanie nie napotykają trudności dla uczniów, dodanie korzeni, podobnie jak ich odejmowanie, czasami prowadzi do zamieszania. A wszystko dlatego, że chcę wykonywać te operacje bez względu na znak główny. I tutaj zaczynają się błędy.

Jakie są zasady dodawania i odejmowania?
Najpierw musisz pamiętać dwa kategoryczne "nie":
- nie dodawaj i nie odejmuj korzeni, np liczby pierwsze to znaczy, że nie można pisać sumowanych wyrażeń radykalnych z jednym znakiem i wykonywać z nimi operacji matematycznych;
- nie można dodawać i odejmować korzeni za pomocą różnych wskaźników, takich jak kwadrat i sześcienny.
Dobry przykład pierwszego zakazu: √6 + √10 ≠ √16, ale √ (6 + 10) = √16 .
W drugim przypadku lepiej ograniczyć się do uproszczenia samych korzeni. I w odpowiedzi na pozostawienie ich kwoty.
Teraz zasady
- Znajdź i zgrupuj podobne korzenie. Oznacza to, że ci, którzy mają nie tylko te same liczby pod radykałem, ale sami mają ten sam wskaźnik.
- Aby wykonać dodanie korzeni, zjednoczonych w jednej grupie przez pierwsze działanie. Jest łatwy do wdrożenia, ponieważ wystarczy dodać wartości stojące przed rodnikami.
- Wyodrębnij korzenie w tych terminach, w których wyrażenie radykalne tworzy cały kwadrat. Innymi słowy, nie pozostawiaj niczego pod znakiem radykała.
- Uprość wyrażenie. Aby to zrobić, musisz rozłożyć je na czynniki pierwsze i sprawdzić, czy nie dadzą pola o dowolnej liczbie. Jest oczywiste, że tak jest w przypadku pierwiastka kwadratowego. Kiedy wykładnik wynosi trzy lub cztery, czynniki pierwsze powinny dać sześcian lub czwartą potęgę liczby.
- Usuń z mnożnika radykalnego znaku, który daje cały stopień.
- Sprawdź, czy podobne terminy pojawiają się ponownie. Jeśli tak, wykonaj ponownie drugą czynność.
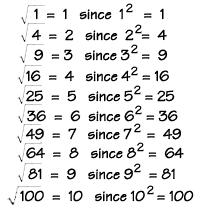
W sytuacji, gdy zadanie nie wymaga dokładnej wartości korzenia, można je obliczyć na kalkulatorze. Niekończąca się część dziesiętna, która będzie wyświetlana w oknie, okrągła. Najczęściej robi się to do setnej. A następnie wykonaj wszystkie operacje dla ułamki dziesiętne.
Ad
Zalecenie: po rozpadzie na czynniki pierwsze należy sprawdzić. Oznacza to, że należy je pomnożyć i sprawdzić, czy uzyskano oryginalną wartość.
To wszystko informacje o tym, jak jest wykonywane dodawanie korzeni. Poniższe przykłady ilustrują powyższe.
Pierwsze zadanie
Oblicz wartość wyrażeń:
a) √2 + 3√32 + ½ √128 - 6√18;
b) √75 - √147 + √48 - 1/5 √300;
c) √275 - 10√11 + 2√99 + √396.
Decyzja.
a) Jeśli zastosujesz powyższy algorytm, jasne jest, że dla pierwszych dwóch akcji w tym przykładzie nic nie ma. Ale możesz uprościć niektóre radykalne wyrażenia.
Na przykład 32 jest rozłożone na dwa czynniki 2 i 16; 18 będzie równe iloczynowi 9 i 2; 128 to 2 na 64. Biorąc to pod uwagę, wyrażenie będzie napisane w ten sposób:
√2 + 3√ (2 * 16) + ½ √ (2 * 64) - 6 √ (2 * 9).
Teraz musimy usunąć z radykalnego znaku te czynniki, które dają kwadrat liczby. Jest to 16 = 4 2 , 9 = 3 2 , 64 = 8 2 . Wyrażenie będzie wyglądało jak:
√2 + 3 * 4√2 + ½ * 8 √2 - 6 * 3√2.
Potrzebujesz trochę łatwiej pisać. Aby to zrobić, pomnóż współczynniki przed głównymi znakami:
√2 + 12√2 + 4 √2 - 12√2.
W tym wyrażeniu wszystkie terminy okazały się podobne. Dlatego wystarczy spasować. Odpowiedź będzie: 5√2.
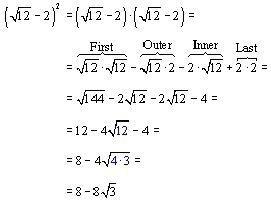
b) Podobnie jak w poprzednim przykładzie, dodanie korzeni zaczyna się od ich uproszczenia. Radykalne wyrażenia 75, 147, 48 i 300 będą reprezentowane przez następujące pary: 5 i 25, 3 i 49, 3 i 16, 3 i 100. Każda z nich ma numer, który można usunąć ze znaku głównego:
Ad
5√5 - 7√3 + 4√3 - 1/5 * 10√3.
Po uproszczeniu otrzymujemy odpowiedź: 5√5 - 5√3. Można go pozostawić w tej formie, ale lepiej jest wyjąć wspólny współczynnik 5 dla wspornika: 5 (√5 - √3).
c) I znowu faktoring: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. Po usunięciu czynników ze znaku głównego uzyskujemy:
5√11 - 10√11 + 2 * 3√11 + 6√11. Po wprowadzeniu takich warunków otrzymujemy wynik: 7√11.
Przykład z wyrażeniami ułamkowymi
√ (45/4) - √20 - 5√ (1/18) - 1/6 √245 + √ (49/2).

Czynniki będą musiały rozłożyć następujące liczby: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Podobne do tych już rozważonych, musisz usunąć czynniki ze znaku głównego i uprościć wyrażenie:
3/2 √5 - 2√5 - 5/3 √ (½) - 7/6 √5 + 7 √ (½) = (3/2 - 2 - 7/6) √5 - (5/3 - 7 ) √ (½) = - 5/3 √5 + 16/3 √ (½).
Wyrażenie to wymaga pozbycia się nieracjonalności w mianowniku. Aby to zrobić, pomnóż przez √2 / √2 drugi termin:
- 5/3 √5 + 16/3 √ (½) * √2 / √2 = - 5/3 √5 + 8/3 √2.
Dla kompletności działania konieczne jest wybranie całkowitej liczby czynników przed korzeniami. W pierwszym jest równy 1, w drugim - 2.