Podział przez zero. Fascynująca matematyka

Liczbę 0 można przedstawić jako rodzaj granicy oddzielającej świat liczb rzeczywistych od wyobrażonych lub negatywnych. Ze względu na niejednoznaczną pozycję wiele operacji o tej wartości numerycznej nie podlega logice matematycznej. Niemożliwość dzielenia przez zero jest żywym przykładem. A rozwiązane operacje arytmetyczne z zerem mogą być wykonywane przy użyciu ogólnie akceptowanych definicji.

Historia zero

Zero jest punktem odniesienia we wszystkich standardowych systemach obliczeniowych. Europejczycy zaczęli używać tej liczby stosunkowo niedawno, ale mędrcy Starożytne Indie używał zera przez tysiąc lat, zanim europejscy matematycy regularnie używali pustej liczby. Nawet przed Indianami zero było obowiązkową wartością w systemie liczbowym Majów. Ci Amerykanie używali rachunku dwunastniczego, a przy zeru zaczynali pierwszego dnia każdego miesiąca. Interesujące jest to, że w języku Majów znak oznaczający "zero" całkowicie zbiegł się ze znakiem określającym "nieskończoność". Tak więc starożytni Majowie doszli do wniosku, że ilości te są identyczne i niepoznawalne.

Operacje matematyczne z zerem

Standardowe operacje matematyczne z zerem można zredukować do kilku reguł.

Dodawanie: jeśli zero zostanie dodane do dowolnej liczby, to nie zmieni jej wartości (0 + x = x).

Odejmowanie: podczas odejmowania zera od dowolnej liczby, wartość odejmowanego pozostaje niezmieniona (x-0 = x).

Mnożenie: dowolna liczba pomnożona przez 0 daje 0 w produkcie (a * 0 = 0).

Podział: zero można podzielić przez dowolną liczbę, która nie jest równa zero. W tym przypadku wartość takiego ułamka będzie równa 0. Podział na zero jest zabroniony.

Potęgowanie. Tę czynność można wykonać dowolnym numerem. Dowolna liczba podniesiona do stopnia zero da 1 (x ⁰ = 1).

Zero wynosi 0 do dowolnego stopnia (0 ^a = 0).

W tym przypadku natychmiast powstaje sprzeczność: wyrażenie 0 ⁰ nie ma sensu.

Paradoksy matematyki

Fakt, że podział przez zero jest niemożliwy, wiele osób wie ze szkoły. Ale z jakiegoś powodu niemożliwe jest wyjaśnienie przyczyny takiego zakazu. W rzeczywistości, dlaczego nie istnieje formuła dzielenia przez zero, ale inne działania z tą liczbą są całkiem rozsądne i możliwe? Odpowiedź na to pytanie udzielają matematycy.

Chodzi o to, że zwykłe operacje arytmetyczne, które uczniowie uczą się w szkole podstawowej, nie są tak naprawdę równe prawom, jak nam się wydaje. Wszystkie proste operacje z liczbami można zredukować do dwóch: dodawanie i mnożenie. Działania te stanowią istotę samej koncepcji liczby, podczas gdy pozostałe operacje opierają się na wykorzystaniu tych dwóch.

Dodawanie i mnożenie

Weź standardowy przykład odejmowania: 10-2 = 8. W szkole jest to po prostu proste: jeśli dwa przedmioty zostaną zabrane z dziesięciu przedmiotów, osiem pozostanie. Ale matematycy patrzą na tę operację zupełnie inaczej. W końcu taka operacja, jak odejmowanie, nie istnieje dla nich. Ten przykład można zapisać w inny sposób: x + 2 = 10. Dla matematyków nieznana jest różnica tylko liczba który należy dodać do dwóch, aby uzyskać osiem. Nie trzeba tu odejmować, wystarczy znaleźć odpowiednią wartość liczbową.

Mnożenie i dzielenie są uważane za takie same. W przykładzie 12: 4 = 3 można zrozumieć, że chodzi o podzielenie ośmiu obiektów na dwie równe grupy. Ale w rzeczywistości jest to tylko odwrócona formuła zapisu 3x4 = 12. Takie przykłady podziału można podać bez końca.

Przykłady podziału przez 0

Tutaj staje się to trochę jasne dlaczego nie można dzielić przez zero. Mnożenie i dzielenie przez zero podlega własnym regułom. Wszystkie przykłady podziału tej ilości można sformułować jako 6: 0 = x. Ale jest to odwrócony zapis wyrażenia 6 * x = 0. Ale, jak wiadomo, każda liczba pomnożona przez 0 daje tylko 0 w produkcie, właściwość ta jest wpisana w samą koncepcję wartości zerowej.

Okazuje się, że nie ma takiej liczby, która po pomnożeniu przez 0 daje jakąś namacalną wartość, czyli to zadanie nie ma rozwiązania. Odpowiedzi tej nie należy się obawiać, jest to naturalna odpowiedź na zadania tego typu. Po prostu pisanie 6: 0 nie ma sensu i nie potrafi niczego wyjaśnić. Krótko mówiąc, to wyrażenie można wytłumaczyć bardzo nieśmiertelnym "dzielenie przez zero jest niemożliwe".

Czy jest operacja 0: 0? Rzeczywiście, jeśli operacja mnożenia przez 0 jest legalna, to można ją zerować przez zero? W końcu równanie postaci 0x 5 = 0 jest całkowicie legalne. Zamiast numeru 5 możesz umieścić 0, produkt tego się nie zmieni.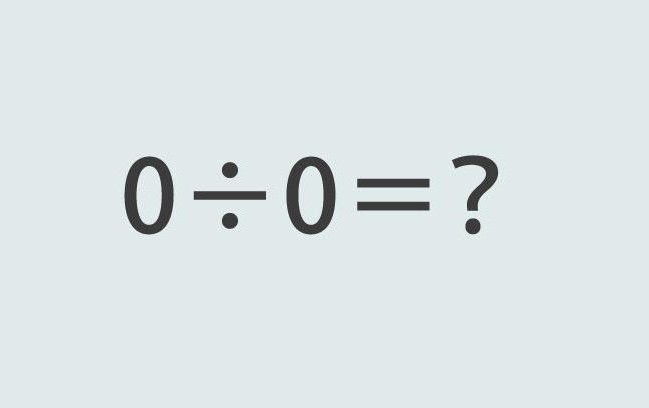

Rzeczywiście, 0x0 = 0. Ale nadal nie można dzielić przez 0. Jak już wspomniano, podział jest po prostu odwrotnym mnożeniem. Tak więc, jeśli w przykładzie 0x5 = 0, musimy określić drugi czynnik, otrzymamy 0x0 = 5. Lub 10. Lub nieskończoności. Dzielenie nieskończoności przez zero - jak ci się podoba?

Ale jeśli jakaś liczba pasuje do wyrażenia, to nie ma sensu, nie możemy wybrać jednego z nieskończonego zbioru liczb. A jeśli tak, oznacza to, że wyrażenie 0: 0 nie ma sensu. Okazuje się, że nawet samego zera nie da się podzielić przez zero.

Wyższa matematyka

Dzielenie przez zero to ból głowy w matematyce szkolnej. Studiował na uczelniach technicznych analiza matematyczna nieznacznie rozszerza pojęcie zadań, które nie mają rozwiązania. Na przykład do już znanego wyrażenia 0: 0 dodano nowe, które nie mają rozwiązania w szkolnych kursach matematycznych:

• nieskończoność podzielona przez nieskończoność: ∞: ∞;
• nieskończoność minus nieskończoność: ∞ - ∞;
• jednostka podniesiona do nieskończonej mocy: 1 ^∞ ;
• nieskończoność pomnożona przez 0: ∞ * 0;
• kilka innych.

Podstawowe metody rozwiązywania takich wyrażeń są niemożliwe. Ale wyższa matematyka, z powodu dodatkowych możliwości dla wielu podobnych przykładów, dostarcza ostatecznych rozwiązań. Jest to szczególnie widoczne w rozważaniu problemów z teorii ograniczeń.

Niepewność ujawnienia

W teorii granic wartość 0 jest zastępowana przez warunkową nieskończenie małą zmienną. I wyrażenia, w których dzielenie przez zero jest uzyskiwane przez podstawienie pożądanej wartości, są konwertowane. Poniżej znajduje się standardowy przykład ujawnienia limitu za pomocą zwykłych przekształceń algebraicznych:

Jak widać na przykładzie, proste zmniejszenie frakcji powoduje jej wartość do całkowicie racjonalnej odpowiedzi.

Rozważając granice funkcji trygonometrycznych, ich wyrażenia mają tendencję do sprowadzania się do pierwszego znaczącego ograniczenia. Rozważając granice, w których mianownik zmienia się na 0 przy ustalaniu limitu, użyj drugiego znaczącego limitu.

Metoda L'Hôpital

W niektórych przypadkach limity wyrażeń mogą być zastąpione limitem ich pochodnych. Guillaume Lopital - francuski matematyk, założyciel francuskiej szkoły analizy matematycznej. Wykazał, że granice wyrażeń są równe granicom pochodnych tych wyrażeń. W pisaniu matematycznym jego zasada jest następująca.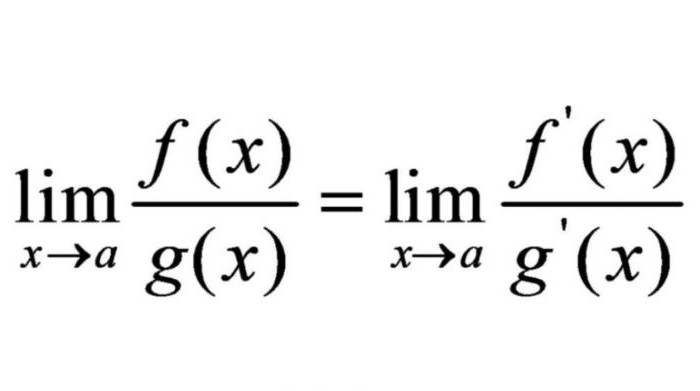

Obecnie metoda L'Hôpital jest z powodzeniem stosowana do rozwiązywania niepewności typu 0: 0 lub ∞: ∞.