Proste i nie tak sposoby obliczania pierwiastka kostki

Ile gniewnych słów wypowiedziano w jego adresie? Czasami wydaje się, że pierwiastek sześcienny jest niesamowicie różny od pierwiastka kwadratowego. W rzeczywistości różnica nie jest tak wielka. Szczególnie jeśli zrozumiesz, że są to tylko szczególne przypadki wspólnego źródła n-tego stopnia.

Ale z jego problemami wydobycia mogą się pojawić. Ale najczęściej są one związane z niewygodnymi obliczeniami.

Co powinieneś wiedzieć o źródle dowolnego stopnia?

Po pierwsze, definicja tej koncepcji. N-ty korzeń jakiegoś "a" to taka liczba, która kiedy potęgowanie n daje oryginał "a".

I są korzenie równe i nieparzyste. Jeśli n jest parzyste, wówczas rodnik może być tylko zerem lub liczbą dodatnią. W przeciwnym razie nie będzie prawdziwej odpowiedzi.

Kiedy stopień jest nieparzysty, wtedy istnieje rozwiązanie dla dowolnej wartości "a". Może być ujemny.

Po drugie, funkcja root może zawsze być zapisana jako stopień, który jest ułamkiem. Czasami jest to bardzo wygodne.

Na przykład "a" do potęgi 1 / n będzie dokładnie korzeniem n-tej potęgi "a". W tym przypadku podstawa stopnia jest zawsze większa od zera.

Podobnie "a" do potęgi n / m będzie reprezentowane jako pierwiastek mth mocy z "a ⁿ ".

Po trzecie, wszystkie akcje ze stopniami są dla nich ważne.

• Można je pomnożyć. Następnie wykładniki sumują się.
• Korzenie można podzielić. Stopień będzie musiał zostać odliczony.
• I podnieść do potęgi. Następnie należy je pomnożyć. Oznacza to, że stopień, który był, do tego, do którego budują.

Jakie są podobieństwa i różnice w kwadratowych i sześciennych korzeniach?

Są podobni, jak bracia, tylko ich stopień jest inny. Zasada ich obliczania jest taka sama, jedyną różnicą jest to, ile razy liczba musi się mnożyć przez siebie, aby uzyskać radykalną ekspresję.

I o znaczącej różnicy powiedziano trochę wyżej. Ale powtórzenie nie będzie zbędne. Kwadrat jest wyodrębniany tylko z liczby nieujemnej. Chociaż łatwo jest obliczyć pierwiastek z ujemnej wartości.

Ekstrakcja korzenia sześciennego na kalkulatorze

Każdy kiedykolwiek to zrobił pierwiastek kwadratowy. A co jeśli stopień "3"?

Na zwykłym kalkulatorze jest tylko przycisk do kwadratu, ale sześcienny nie jest. Pomoże to w prostym wyliczeniu liczb pomnożonych przez trzy razy. Uzyskać radykalną ekspresję? Tak więc to jest odpowiedź. Nie działa? Podnieś ponownie.

A co z formą inżynierską kalkulatora w komputerze? Brawo, istnieje sześcienny korzeń. Ten przycisk można po prostu kliknąć, a program udzieli odpowiedzi. Ale to nie wszystko. Tutaj możesz obliczyć źródło nie tylko 2 i 3 stopni, ale także dowolne. Ponieważ istnieje przycisk, w którym stopień korzenia to "y". Oznacza to, że po naciśnięciu tego klawisza należy wprowadzić inny numer, który będzie równy poziomowi korzenia, a dopiero potem "=".

Ręczna ekstrakcja korzenia kostki

Ta metoda jest wymagana, gdy kalkulator nie jest dostępny lub nie możesz go użyć. Następnie, aby obliczyć pierwiastek kostki z liczby, będzie to wymagać wysiłku.

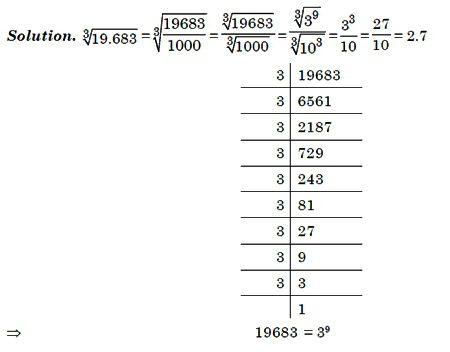
Najpierw sprawdź, czy pełna kostka nie została uzyskana z żadnej wartości całkowitej. Może korzeń jest 2, 3, 5 lub 10 w trzecim stopniu?

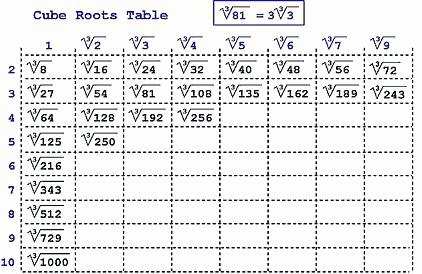
W przeciwnym razie musisz być traktowany jako kolumna. Algorytm nie jest najłatwiejszy. Ale jeśli ćwiczysz trochę, działania będą łatwo zapamiętywane. A obliczenie korzenia kostki nie będzie już problemem.

1. Mentalnie podziel wyraz radykalny na grupy składające się z trzech cyfr z przecinka dziesiętnego. Najczęściej potrzebna jest część ułamkowa. Jeśli nie, to zera muszą się skończyć.
2. Określ liczbę, której sześcian jest mniejszy od całkowitej części wyrażenia radykalnego. Napisz to w pośredniej odpowiedzi powyżej znaku głównego. I w tej grupie, aby umieścić swoją kostkę.
3. Wykonaj odejmowanie.
4. Dodaj pierwszą grupę cyfr do reszty.
5. W wersji roboczej wpisz wyrażenie: a ² * 300 * x + a * 30 * x ² + x ³ . Tutaj "a" jest odpowiedzią pośrednią, "x" jest liczbą, która jest mniejsza niż wynikowa równowaga z przypisanymi do niej liczbami.
6. Liczba "x" musi być zapisana po przecinku pośredniej odpowiedzi. I wartość całego wyrażenia do zapisu pod porównywalnym saldem.
7. Jeśli dokładność jest wystarczająca, obliczenia zostają zatrzymane. W przeciwnym razie musisz powrócić do pozycji nr 3.

Ilustracyjny przykład obliczenia sześciennego pierwiastka

Jest to konieczne, ponieważ opis może wydawać się skomplikowany. Poniższy rysunek pokazuje, jak wyodrębnić pierwiastek z 15 do najbliższej setnej.

Jedyną trudnością tej metody jest to, że z każdym krokiem liczby wzrastają wielokrotnie i trudniej jest liczyć się na pasku.

1. 15> 2 ³ , następnie pod częścią całkowitą 8 jest zapisany, a powyżej katalogu głównego 2.
2. Po odjęciu od 15 ósemki otrzymujemy pozostałą 7. Do tego musimy dodać trzy zera.
3. a = 2. Dlatego: 2 ² * 300 * x + 2 * 30 * x ² + x ³ <7000 lub 1200 x + 60 x ² + x ³ <7000.
4. Metoda wyboru okazuje się, że x = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
5. Odejmowanie daje 1176, a liczba 4 pojawia się nad korzeniem.
6. Przypisz trzy zera do reszty.
7. a = 24. Następnie 172800 x + 720 x ² + x ³ <1176000.
8. x = 6. Obliczenie wyrażenia daje wynik 1062936. Saldo: 113064, powyżej korzenia 6.
9. Ponownie przypisz zera.
10. a = 246. Nierówność uzyskuje się w następujący sposób: 18154800x + 7380x ² + x ³ <113064000.
11. x = 6. Obliczenia podają liczbę: 109194696, Balans: 3869304. Nad korzeniem 6.

Odpowiedź brzmi: 2, 466. Ponieważ odpowiedź musi być udzielona setnym, należy zaokrąglić: 2.47.

Niezwykły sposób na wyodrębnienie korzenia sześciennego

Może być używany, gdy odpowiedź jest liczbą całkowitą. Następnie pierwiastek sześcienny jest wyodrębniany poprzez rozkład radicand na nieparzyste terminy. Ponadto takie warunki powinny stanowić minimalną możliwą liczbę.

Na przykład 8 jest reprezentowane przez sumę 3 i 5. A 64 = 13 + 15 + 17 + 19.

Odpowiedź będzie liczbą równą liczbie terminów. Zatem sześcienny pierwiastek równy 8 będzie równy dwóm, a od 64 do czterech.

Jeśli kosztuje 1000 pod korzeniem, wówczas jego rozkład na warunki będzie wynosił 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Łącznie 10 terminów. To jest odpowiedź.