Co to jest - stożek w geometrii. Stożek prosty z okrągłą podstawą i jej charakterystyką

Geometria przestrzenna, której przebieg odbywa się w szkole średniej, bada właściwości i właściwości różnych kształtów geometrycznych w trzech wymiarach. Jedną z takich znanych postaci jest stożek. To jest stożek, jakie elementy opisuje i jakie właściwości posiada, artykuł odpowie na te pytania.

Stożek w geometrii

Z punktu widzenia stereometrii stożek jest postacią utworzoną w przestrzeni poprzez połączenie prostych odcinków pewnego punktu z krzywą w płaszczyźnie. Ta krzywa nazywana jest directrix, czyli przewodnikiem. Ogranicza to kształt podstawy. Directrix może być zamkniętą linią, taką jak elipsa lub okrąg, lub nie może być zamknięta, jak hiperbola lub parabola. Wszystkie segmenty łączące directrix z wyżej wymienionym punktem przestrzeni są nazywane generatrices lub generators. Zbiór generatorów definiuje stożkową powierzchnię, a punkt, z którego wychodzą, nazywany jest wierzchołkiem stożka.

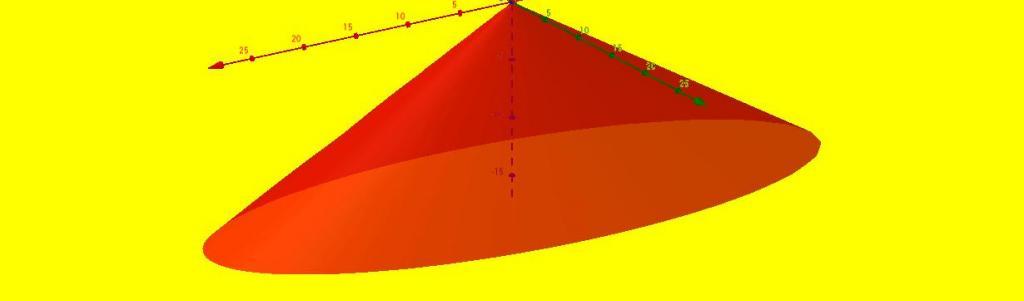
Stożek ma postać jednego wierzchołka, bez krawędzi i składa się z dwóch powierzchni (płaskiej podstawy i bocznej stożkowej powierzchni). Eliptyczny stożek pokazano na powyższym rysunku.

Okrągły lub okrągły stożek

Pod słowem "runda" w tytule przedmiotu rozumiemy figurę, której podstawą jest okrąg. W przeciwieństwie do innych rodzajów stożków, w wyniku obrotu można uzyskać okrągłą figurę. Poniższy rysunek przedstawia ten proces.

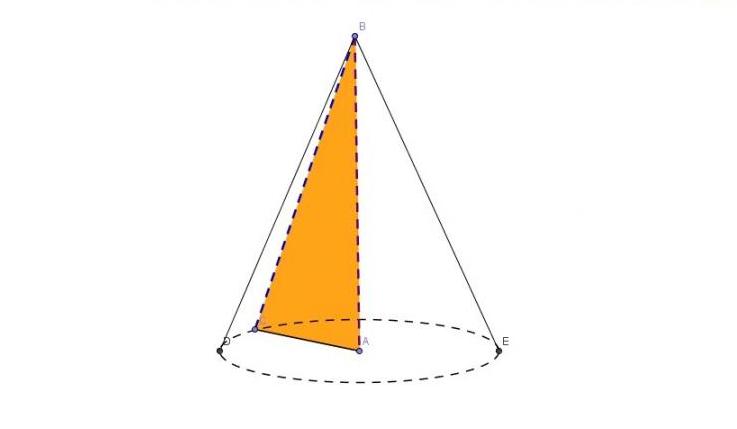
Pokrótce wyjaśnijmy, co pokazuje rysunek. Trójkąt ABC jest prostokątny. Jeśli zostanie obrócony wokół nogi AB, noga AC opisuje jedną powierzchnię stożka, podstawę i przeciwprostokątną BC spowoduje powstanie stożkowej powierzchni w wyniku obrotu.

Stożek pokazany na rysunku jest nie tylko okrągły, ale również prosty. Ta druga właściwość jest ważna do rozważenia podczas wykonywania obliczeń parametrów liniowych, powierzchni i objętości figury.

Geometryczny kształt stożka jest prosty, jeśli wysokość h spada dokładnie w środku podstawy (w tym przypadku wysokość jest odcinkiem AB, a środek podstawy jest punktem A). Jeśli określony warunek nie jest spełniony, liczba ta nazywana jest ukośną. Ukośne i proste stożki są pokazane poniżej dla jasności.

Wiele otaczających nas obiektów, takich jak stożki lodów, pasiasty stożek drogowy lub lejek do wlewania cieczy przez wąskie otwory, mają kształt stożka z okrągłą podstawą.

Następnie rozważamy charakterystyki ilościowe prostego stożka z okrągłą podstawą.

Wymiary liniowe figury i kąt w podstawie

Wymiary liniowe stożka są zbiorem parametrów, które pozwalają jednoznacznie zdefiniować figurę w przestrzeni. Są to następujące:

• promień podstawy r;
• wysokość h;
• generatrix g.

Zauważ, że dla rozważanego rodzaju stożka wszystkie tworzące są sobie równe i przecinają podstawę figury pod tym samym kątem.

Oprócz powyższych parametrów liniowych stożek charakteryzuje się także kątem φ między generatorem a podstawą.

Wszystkie te cechy są powiązane ze sobą za pomocą następujących podstawowych równań:

g = √ (h ² + r ² );

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ)

Te równości można zapisać niezależnie, jeśli weźmiemy pod uwagę trójkąt prostokątny wewnątrz stożka i przywołujemy definicje wskazanych funkcji trygonometrycznych.

Powierzchnia

Obszar podstawy i stożkowa powierzchnia są ważną cechą stożka. Jest jaśniejsze i łatwiejsze badanie powierzchni figury nie w trójwymiarowej, ale w dwuwymiarowej przestrzeni. Aby to zrobić, wykonaj tak zwane wzorce skanowania. Możesz sobie wyobrazić proces jego odbioru w następujący sposób: Załóżmy, że jest stożek wykonany z papieru. Najpierw przecinamy jego podstawę wzdłuż obwodu, a następnie przecinamy stożkową powierzchnię wzdłuż generatora i rozłożymy ją. Otrzymaliśmy skan stożka, który pokazano poniżej na rysunku.

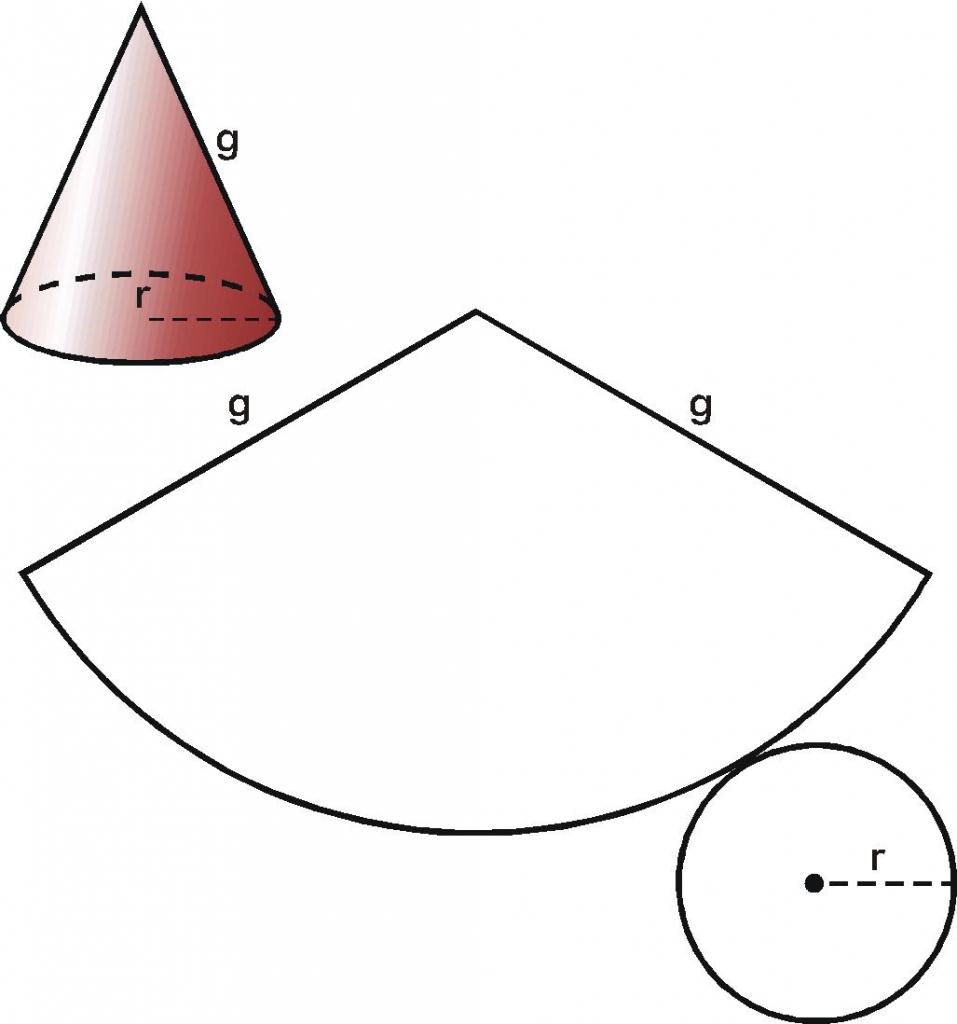
Obszar całego ruchu S jest równy:

S = S _o + S _b

Tam, gdzie pierwszym terminem (S _o ) jest obszar koła, drugi człon (S _b ) jest obszarem okręgu odzwierciedlającego stożkową powierzchnię. Wartość S _o oblicza się według następującego wzoru:

S _o = pi * r ²

W przypadku sektora kołowego sytuacja jest bardziej skomplikowana. Jest ograniczony przez dwa promienie, których długość jest równa generatrix g, i jeden łuk odpowiadający obwodowi koła podstawowego. Te informacje numeryczne pozwalają jednoznacznie określić obszar sektora. Nie pójdziemy do obliczeń matematycznych, ale natychmiast podamy ostateczną formułę dla S _b :

S _b = pi * r * g

Porównanie zapisanych formuł dla S _b i S _o sugeruje, że powierzchnia boczna jest zawsze większa niż dla podstawy za pomocą g / r.

Wzór na całkowitą powierzchnię jest następujący:

S = pi * r * (r + g)

Rozmiar ciała

Stożek jest postacią przestrzenną, więc ma pewną objętość. Numerycznie odpowiada obszarowi przestrzeni ograniczonemu przez stożkową powierzchnię i okrągłą podstawę. Aby określić objętość stożka, należy użyć następującego wyrażenia:

V = 1/3 * S _o * h

Zastępując w tym wyrażeniu wzór S _o , otrzymujemy:

V = 1/3 * pi * r ² * godz

Niektórzy czytelnicy mogli zauważyć, że wzór na objętość stożka odpowiada tej dla piramidy. Ta zbieżność nie jest przypadkowa, ponieważ kształty tych figur stają się identyczne, jeśli liczba krawędzi prostej piramidy wzrasta do nieskończoności.