Bezpłatne wibracje. Informacje ogólne

W tym artykule porozmawiamy o swobodnych oscylacjach. Rozważcie ich przykłady: wahadła matematyczne i wiosenne, a także obwód oscylacyjny.

Drgania mechaniczne

Ruch oscylacyjny lub mechaniczne oscylacje nazywa się ruchem ciał lub zmianą stanu, która powtarza się z czasem. Przykładami mechaniki mogą być oscylacje wahadeł, strun, wyważarek zegarów, membran głośnikowych, mostów i innych konstrukcji.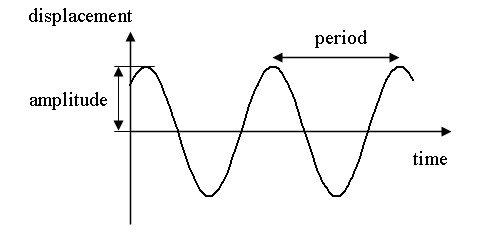

Ruch oscylacyjny nazywany jest periodycznym, jeśli wartości wielkości fizycznych, które zmieniają się podczas oscylacji, powtarzają się w równych odstępach czasu.

Minimalny interwał (okres) czasu, po którym pozycja ciała jest powtarzana podczas ruchu oscylacyjnego nazywany jest okresem oscylacji T. Liczba oscylacji, jaką ciało wykonuje w jednostce czasu, nazywana jest częstotliwością oscylacji ν .

Harmoniczne

Spośród różnych ruchów oscylacyjnych ważne są harmoniczne ruchy oscylacyjne.

Harmonię nazywa się oscylacją, podczas której punkt materialny odbiega od pozycji równowagi zgodnie z prawem sinus lub cosinus.

Znaczenie tego ruchu polega na tym, że wiele ruchów oscylacyjnych w przyrodzie jest blisko harmonicznych, a także dlatego, że złożone wibracje można rozłożyć na harmoniczne. Piszemy przesunięcie punktu materialnego podczas ruchu harmonicznego:

x = Asin (ωt + φ ₀ )

Litera " x" oznacza odchylenie punktu oscylującego od położenia równowagi. Maksymalne przesunięcie z pozycji równowagi nazywa się amplitudą. W naszym przypadku x _max = A. Argument (ωt + φ ₀ ) nazywany jest fazą oscylacji, a wartość φ ₀ - początkowa faza oscylacji. Faza pozwala określić przesunięcie punktu w określonym momencie.

Okres oscylacji harmonicznej T , z uwagi na to okres oscylacji faza zmieni się na 2π , można obliczyć za pomocą następującego wzoru:

T = 2π / ω.

Częstotliwość swobodnych oscylacji wynosi:

ν = 1 / T = ω / 2π.

Prędkość punktu z oscylacjami harmonicznymi określana jest jako pierwsza pochodna przesunięcia czasowego:

v = dx / dt = Acocos (ωt + φ ₀ ).

Przyspieszenie punktu z oscylacjami harmonicznymi występuje jako druga pochodna przesunięcia czasowego:

a = dv / dt = Aω ² cos (ωt + φ ₀ ).

Bezpłatne

Jeśli ciało w systemie oscylacyjnym zostanie wyprowadzone z równowagi i uwolnione, wówczas wykona tak zwane swobodne oscylacje, które zawsze są tłumione.

Aby badać oscylacje o różnej naturze, często używają urządzeń, zwanych oscyloskopami. Oscyloskop (z łaciny Oscillo - "wahaj się" i grecki, wykres - "napisz") - urządzenie do obserwacji oscylacji i zapisywania ich w formie graficznej.

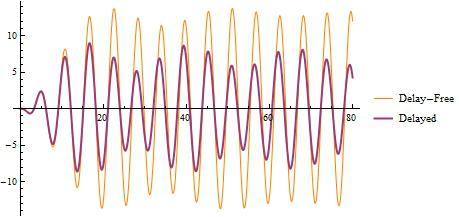
Amplituda oscylacji w systemach rzeczywistych maleje wraz z upływem czasu, a oscylacje w końcu ustają, dlatego też swobodne oscylacje są zawsze tłumione.

Okres oscylacji nie zależy od ich amplitudy, ponieważ w prawdziwych układach mechanicznych zawsze występuje utrata energii mechanicznej.

Badanie wolnych drgań w układzie "obciążenie-sprężyna", przy braku strat energia mechaniczna można wywnioskować, że okres takich oscylacji jest określony przez wzór:

T = 2π / ω,

gdzie ω jest częstotliwością cykliczną.

Częstotliwość wolnych oscylacji jest mierzona według wzoru:

ν = 1 / T = ω / 2π.

Wahadło matematyczne

Wahadło matematyczne jest uważane za ciało punktowe zawieszone na nierozciągliwej i nieważącej nici. Wahadło matematyczne jest pojęciem abstrakcyjnym, ponieważ po pierwsze, nie ma w naturze żadnych ciał punktowych, a po drugie, nie ma absolutnie nierozciągliwych i nieważących nici. Jednak z pewnym przybliżeniem, matematyczny wahadło można uznać za kulę zawieszoną na nitce. Gdy kula znajduje się w stanie równowagi, działa na nią siła grawitacji i siła sprężystości nici, które równoważą się nawzajem, innymi słowy, wypadkowa tych sił wynosi zero.

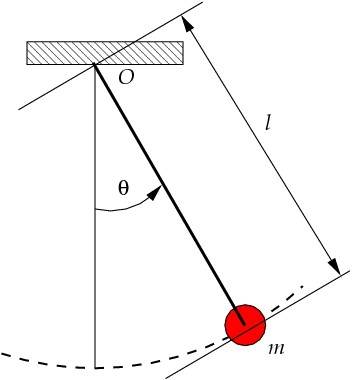
Okres oscylacji matematycznego wahadła można obliczyć według wzoru:

T = 2π / ω,

gdzie cykliczna częstotliwość swobodnych oscylacji ω ² = l / g, a l to długość nici.

Zgodnie z formułą można wnioskować, że okres oscylacji matematycznego wahadła nie zależy od masy ciała, ale zależy tylko od długości zawieszenia i przyspieszenia swobodnego spadania.

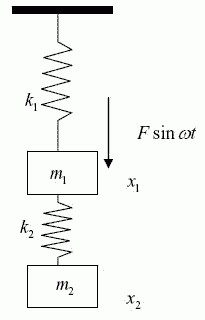
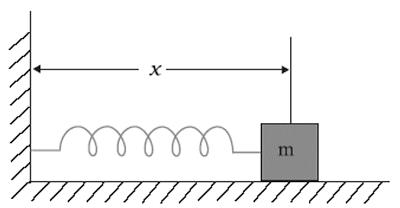
Wahadło sprężynowe

Innym przykładem harmonicznych drgań swobodnych są drgania ciała na sprężynie. W stanie równowagi sprężyna nie jest jeszcze zdeformowana, siła sprężysta nie działa na ciało. Siła tarcia między ciałem a podporą również wynosi zero. Siła przyciągania równoważona jest siłą reakcji wsparcia. Jeśli ciało zostanie wyprowadzone z równowagi, przesuwając je wzdłuż osi OX w odległości x = ± A , a następnie zwalniając, wahadło będzie swobodnie oscylować pod działaniem siły sprężystej, a swobodne wahania wahadła będą następować zgodnie z prawem x = Asinwt.

Okres wolnych oscylacji wahadła na sprężynie jest równy:

T = 2π / ω,

gdzie cykliczna częstotliwość oscylacji ω ² = k / m, k to sztywność sprężyny, m to masa ciała.

Jak widać z tego wzoru, nie zależy od okresu i częstotliwości oscylacji wahadła sprężyny przyspieszenie grawitacyjne i są określane tylko przez masę zawieszonego korpusu i sztywność sprężyny.

Oscylacje elektryczne w obwodzie

Obwód elektryczny, w którym możliwe są swobodne oscylacje elektromagnetyczne, nazywany jest obwodem oscylacyjnym. Składa się z kondensatora o pojemności C, cewki o indukcyjności L i rezystora o rezystancji R (w rzeczywistym obiegu technicznym oporność cewki i przewody łączące pełnią rolę rezystora).

Prawo Ohma dla obwodu zamkniętego, które nie zawiera zewnętrznego źródła prądu, i w którym występują wolne drgania elektromagnetyczne, jest napisane w tej formie:

JR + U = - L (dJ / dt),

gdzie U = q / C jest napięciem na kondensatorze, q jest ładunkiem kondensatora, J = dq / dt jest prądem w obwodzie.

Swobodne oscylacje w obwodzie są harmoniczne, dlatego zmieniają się zgodnie z następującymi przepisami:

q (t) = q ₀ cos (ωt + φ ₀ ).